Positive-definite Matrix

In linear algebra, an $n \times n$ Hermitian matrix $A$ is said to be positive definite if the scalar $x^{*}\text{Ax}$ is real and positive for all non-zero column vectors $x$ of $n$ complex numbers. Here $x^{*}$ denotes the conjugate transpose of $x$.

Let $A$ be an $n \times n$ Hermitian matrix. The following properties are equivalent to $A$ being positive definite:

1. All its eigenvalues are positive.

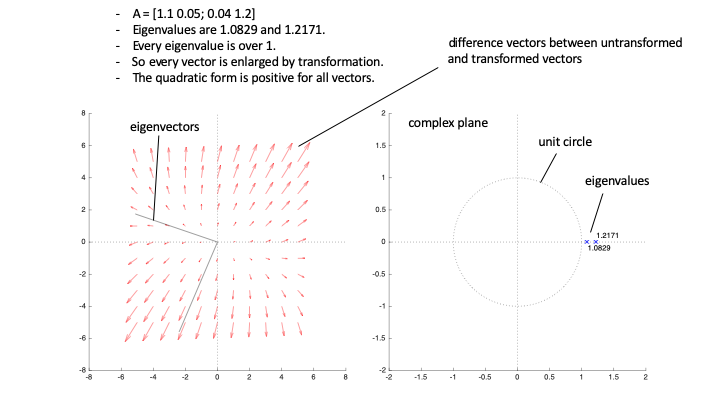
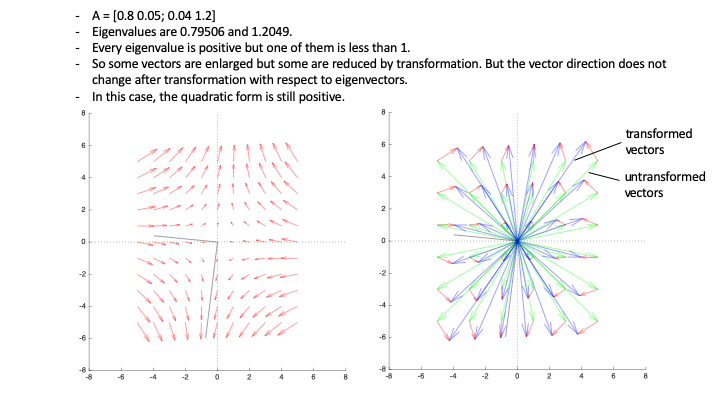
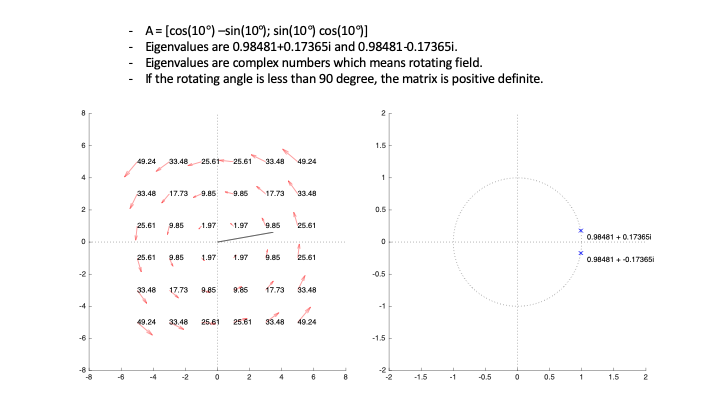
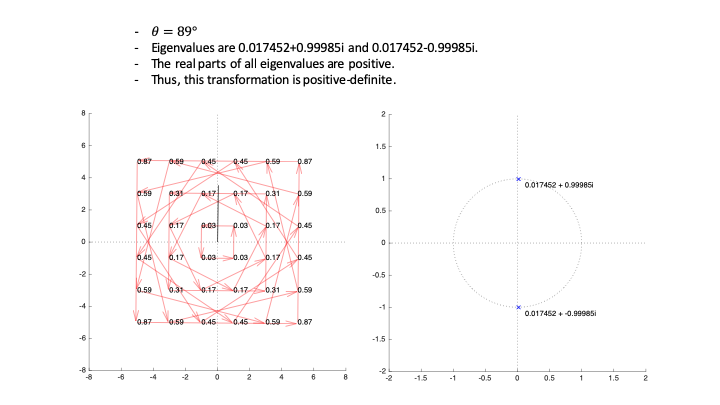
• Eigenvalues are enlargement factors of each eigenvector in geometrical meaning when we consider a matrix the transformation.

• If all eigenvalues are positive, every vector is enlarged by the matrix and, thus, is in the same direction.

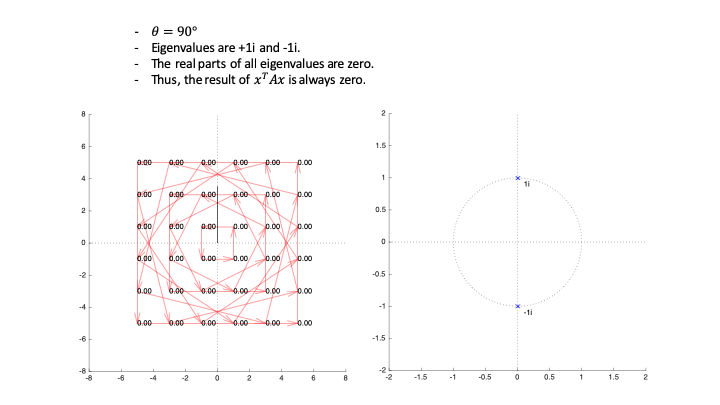
• The equation $\mathbf{x}^{*}\mathbf{\text{Ax}}$ can be seen as the dot product of $\mathbf{x}$ and $\mathbf{\text{Ax}}$, which means untransformed and transformed vectors. Since $\text{Ax}$ is in the same direction, the dot product $x^{*}\text{Ax}$ should be positive.

* MATLAB code can be found here and here.

2. Its leading principal minors are all positive. (Sylvester’s criterion)

3. It has a unique Cholesky decomposition.

• The matrix $A$ is positive definite if and only if there exists a unique lower triangular matrix $L$, with real and strictly positive diagonal elements, such that $A = LL^{*}$.

Negative-definite, semidefinite and indefinite matrices

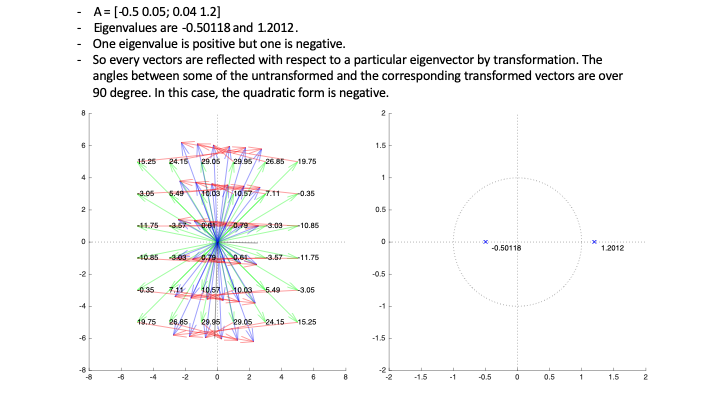
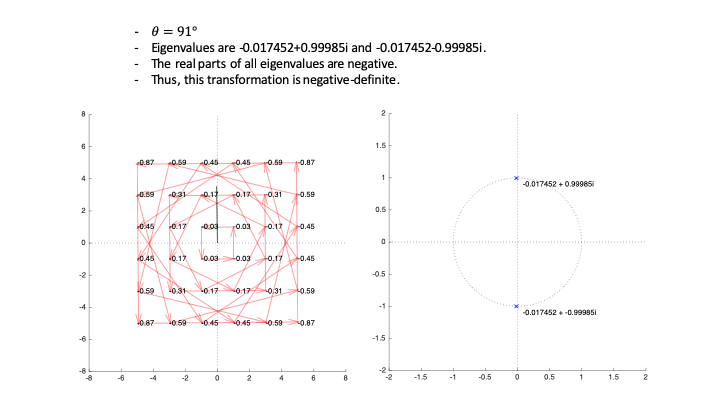
A Hermitian matrix is negative-definite, negative-semidefinite, or positive-semidefinite if and only if all of its eigenvalues are negative, non-positive, or non-negative, respectively.