확률변수의 연산

이번 글에서는 확률변수의 연산에 대하여 알아본다.

앞으로 결정론적 변수를 일반변수(편의상 붙여 쓰기로 한다)로 부르기로 한다.

$1+1=2$이듯이 일반변수와 일반변수를 연산하면 일반변수가 나온다. 즉, 100% 확실한 값을 서로 연산하면 100% 확실한 값이 된다. 그렇다면 일반변수와 확률변수를 연산하면 어떤 값이 나올까? 확률변수가 된다. 다수의 변수를 포함하는 수식에 하나라도 불확실한 값(확률변수)이 포함되면 그 결과는 불확실해지는 것이다. 확률변수와 확률변수를 연산해도 확률변수가 된다. 이를 정리하면 아래와 같이 표현할 수 있다. 여기서 x는 일반적인 연산기호를 나타낸다고 생각하자.

• 일반변수 x 일반변수 = 일반변수
• 일반변수 x 확률변수 = 확률변수
• 확률변수 x 확률변수 = 확률변수

일반변수와 확률변수의 연산

일반변수와 확률변수의 연산에 대하여 알아보자. 가장 대표적인 연산인 사칙연산 중 덧셈과 곱셈을 생각해보자.(뺄셈과 나눗셈은 덧셈 및 곱셈과 동일한 방식으로 계산 가능하다)
이전 글에서 사용한 동전 던지기 결과를 나타내는 확률변수 $X$에 1을 더한 값을 나타내는 확률변수를 $X_+$라고 한다면 $X_+$의 값은 어떻게 될까?

\[X_+=X+1\]

$X$가 0일 때는 $X_+$가 1, $X$가 1일 때는 $X_+$가 2가 될 것이다. 또한 $X$가 0, 1일 때와 동일한 확률로 $X_+$가 각각 1, 2로 발생할 것이다. 따라서 $X_+$의 확률분포 $f_+(x)$는 아래와 같은 수식과 그림으로 표현할 수 있다. 확률분포 $f_+(x)$는 확률분포 $f(x)$에 비하여 수평이동한 것을 알 수 있다.

\[f_+(x)=\begin{cases}\frac{1}{2},&\text{if $x=1$ or $2$}\\0,&\text{otherwise}\end{cases}\]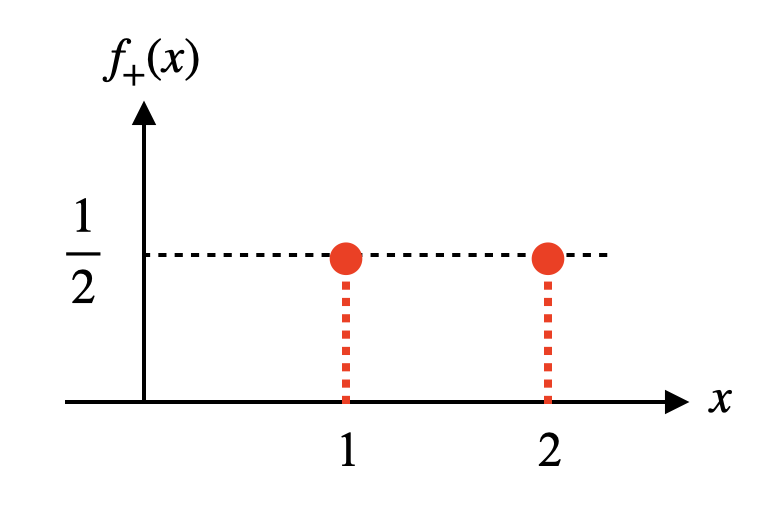

$X$에 2를 곱한 확률변수를 $X_{\times}$라고 한다면 $X_{\times}$의 값을 어떻게 될까?

\[X_{\times}=2X\]

$X$가 0일 때는 $X_{\times}$도 0, $X$가 1이면 $X_{\times}$가 2가 된다. $X_{\times}$가 0, 2일 확률은 각각 $X$가 0, 1일 확률과 같다. 이를 수식과 그림으로 나타내면 아래와 같다. 확률분포 $f_{\times}(x)$는 확률분포 $f(x)$에 비하여 수평방향으로 확대된 것을 알 수 있다.

\[f_{\times}(x)=\begin{cases}\frac{1}{2},&\text{if $x=0$ or $2$}\\0,&\text{otherwise}\end{cases}\]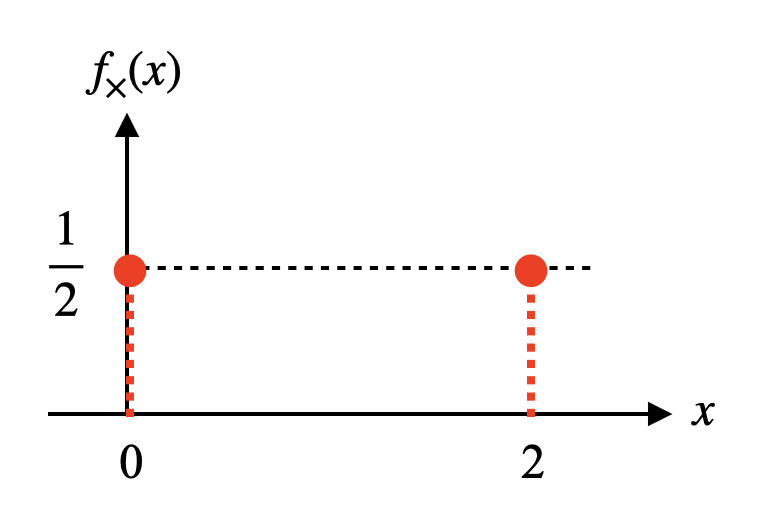

확률변수에 실수를 곱하고 더하는 연산을 일반적으로 아래와 같이 나타낸 수 있다. 이러한 연산을 선형변환(linear transformation)이라고 부른다.

\[Y=aX+b\]

확률변수와 확률변수의 연산

확률변수와 확률변수의 연산은 은근히 까다롭다.(이러한 이유로 일반변수보다 확률변수를 사용하는 것이 어렵게 느껴지는 것 같다.) 먼저 확률변수 $X$와 $X$를 더한 값을 나타내는 확률변수를 $Z_1$이라고 하자. 동전을 두 번 던진 후 그 결과를 더한 것이라고 생각해도 좋다.(두 사건은 서로 독립이라고 가정한다.)

\[Z_1=X+X\]

$Z_1$이 가질 수 있는 값은 총 몇 가지일까? 세 가지이다.[1] 0과 0을 더한 0, 0과 1 또는 1과 0을 더한 1, 1과 1을 더한 2. 그렇다면 $Z_1$이 0, 1, 2일 확률은 어떻게 될까? 두 $X$가 모두 0이거나 모두 1일 확률은 각각 1/2 x 1/2 = 1/4이다. 두 $X$중 하나는 0이고 하나는 1일 확률은 1/2 x 1/2 + 1/2 x 1/2 = 1/2이다. 따라서 $Z_1$의 확률분포 $f_{z1}(x)$는 다음과 같다.

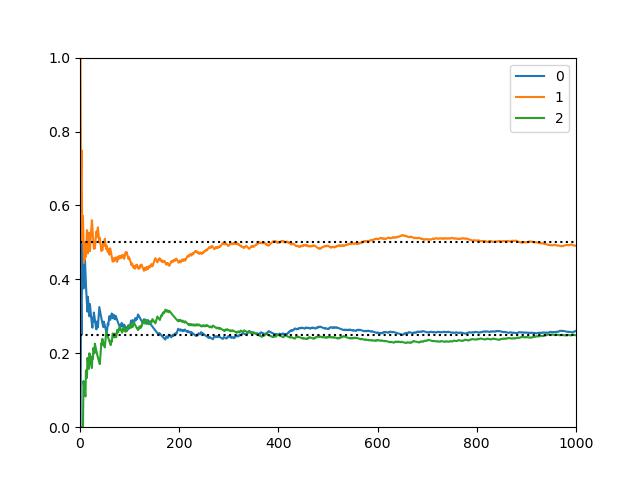
\[f_{z1}(x)=\begin{cases}\frac{1}{4},&\text{if $x=0$ or $2$}\\\frac{1}{2},&\text{if $x=1$}\\0,&\text{otherwise}\end{cases}\]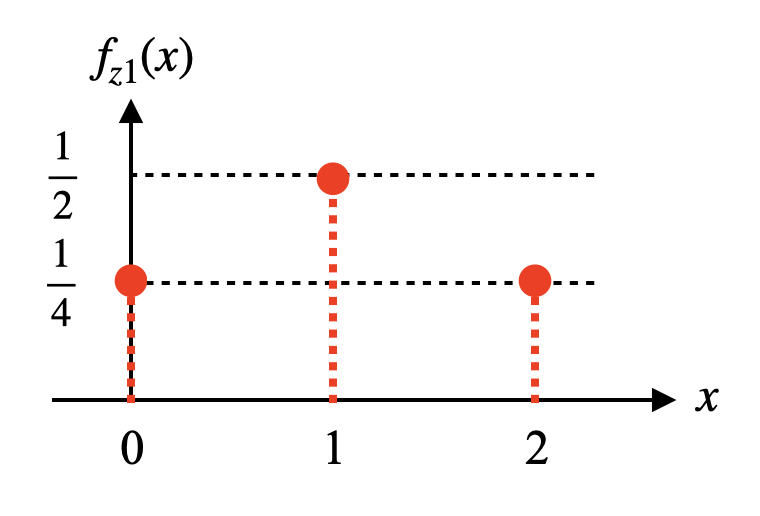

이와 같이 확률변수간의 연산에서는 서로 다른 경우에서 같은 값이 나올 수 있으며(앞에서 0과 1이 나오거나 1과 0이 나오는 서로 다른 경우에 1이라는 같은 값이 나옴) 이들의 확률을 더해주어야 확률분포를 구할 수 있다.(확률변수간의 연산이 까다로운 이유다)

두 $X$를 서로 곱한 값을 $Z_2$라고 하면 $Z_2$의 확률분포도 같은 방법으로 구할 수 있다.(이 경우에는 0이 되는 경우가 3가지가 있어 이들의 확률을 서로 더해준다)

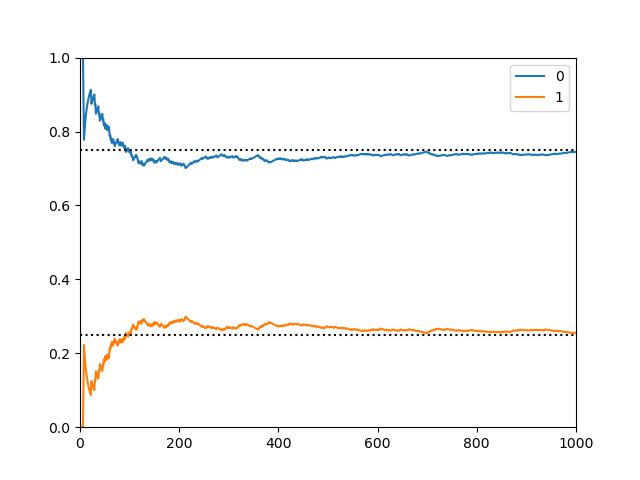
\[Z_2=XX\] \[f_{z2}(x)=\begin{cases}\frac{3}{4},&\text{if $x=0$}\\\frac{1}{4},&\text{if $x=1$}\\0,&\text{otherwise}\end{cases}\]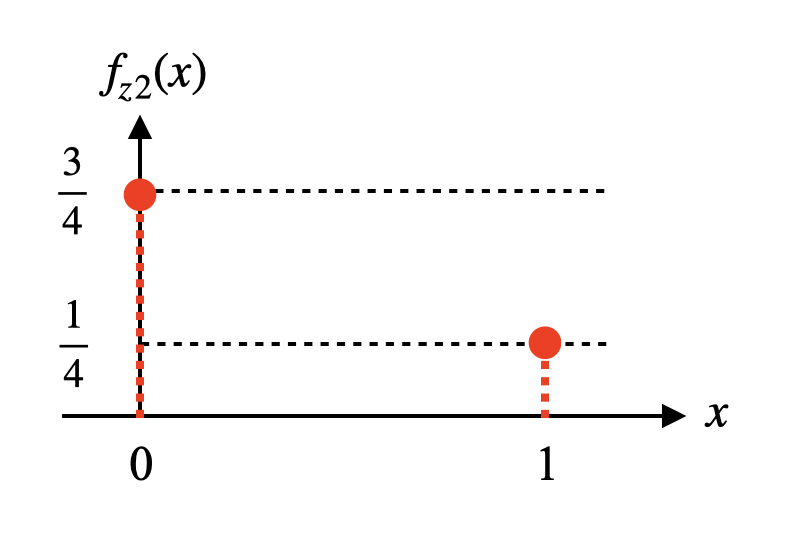

시뮬레이션을 이용한 검증

동전을 두 번 던져 나온 값의 합을 나타내는 확률변수 $Z_1$과 곱을 나타내는 확률변수 $Z_2$가 정말로 앞에서 구한 확률분포와 같은 결과가 나오는지 시뮬레이션으로 검증해보자. 파이썬을 이용하여 이상적인 동전을 두 번 던지는 실험을 1000번 반복하면서 두 값을 더한 값이 0, 1, 2인 비율(확률)과 곱한 값이 0, 1인 비율(확률)의 변화추이를 그래프로 그려보니 아래와 같았다. 1000번의 반복만으로도 앞에서 구한 확률분포에 근접하는 결과를 얻을 수 있었다. 시뮬레이션 소스코드는 [2]에서 볼 수 있다.

확률분포를 구하는 일반적인 방법

새로운 확률변수의 확률분포를 구하는 일반적인 방법은 다음과 같다. 확률변수 $Y$가 확률변수 $X$의 함수라고 가정해보자.

\[Y=g(X)\]

$Y$의 확률분포는 다음과 같이 구할 수 있다. 즉, $g(x)=y$를 만족하는 모든 $x$에 대한 확률의 합이 $Y$가 $y$일 때의 확률이 된다.(어렵게 느껴지면 그냥 넘어가도 좋다)

\[p_Y(y)=\sum_{\{x|g(x)=y\}}p_X(x)\]

이는 이산확률분포를 구하는 방법이며, 연속확률분포를 구하기 위해서는 르벡적분(Legesgue integration)을 사용해야 한다.

그 밖의 연산

확률변수에는 사칙연산 이외에도 여러가지 수학연산을 적용할 수 있다. 예를 들어, 절대값과 최대값이 그 예이다.

\[Y=|X|\] \[Z=\max(X,Y)\]

앞에서 제시한 방법과 동일하게 새로운 확률변수가 가질 수 있는 모든 값에 대하여 각각의 확률을 더하여 확률분포를 구할 수 있다.

주석

[1] $X+X=2X$로 생각하면 안 된다. 이는 동전을 두 번 던졌을 때 앞면, 앞면 또는 뒷면, 뒷면으로 항상 같은 면이 나온다는 의미이며 서로 독립사건이 아닌 경우에 해당한다.
[2] https://github.com/reingel/JProbStats