확률변수란 무엇인가?

확률변수는 확률의 처음과 끝이라고 해도 과언이 아닐 정도로 아주 중요한 개념이다. 이번 글에서는 확률변수란 무엇인지 알아보자.

결정론적 vs 확률론적

지구가 태어나고 수십 억년간 그래 왔듯이 내일 아침에도 해가 뜰 것이다.(내일 갑자기 지구가 멸망하는 스토리는 고려하지 말자) 이와 같이 100% 일어날 사건을 결정론적(deterministic) 사건이라고 표현한다. 반면 “내일 비가 오는지”는 아직 정해지지 않았다.(물론 적은 오차로 예측할 수는 있다) “비가 올 가능성이 높다” 또는 “70% 확률로 온다”와 같이 불확실하게 말할 수 밖에 없다. 이러한 사건을 확률론적(stochastic) 사건이라고 표현한다.

결정론적 사건은 실재하지 않는다. 이전 글에서 설명한 플라톤의 원(circle)과 같이 우리의 관념 속에만 존재한다. 이 세상 모든 물리적 현상은 확률론적이다. 상대성 이론에서 불변의 값이라고 하는 빛의 속도도 아무리 정밀한 장치를 사용하더라도 측정할 때마다 값이 미세하게 다르다. 양자역학에 따르면 이 세상을 구성하는 모든 입자들은 확률론적으로 거동한다.

확률변수

입력값을 두 배로 만들어 출력하는 아주 간단한 컴퓨터 프로그램(또는 함수)을 생각해보자. 입력변수를 $x$, 출력변수를 $y$라고 한다면 이 프로그램은 $y=2x$로 나타낼 수 있다. 변수 $x$가 1이면 변수 $y$는 항상 $2$이다. 이처럼 동일한 조건에서 항상 같은 값을 갖는 변수를 결정론적 변수라고 한다. 그렇다면 시간에 따라 값이 변하는 변수는 어떨까? 변수 $v$가 시간 $t$에 대하여 $v(t)=t^2+2t-1$과 같이 변한다면 $v$는 결정론적 변수일까, 확률론적 변수일까? 결정론적 변수이다. 시간 $t$는 주어지는 값(독립변수)이며 시간이 주어지면 속도가 하나의 값으로 결정되기 때문에 $v$도 결정론적 변수이다. 우리가 그동안 학교에서 배운 대부분의 수식은 결정론적 개념으로 설명되어 있다. 일반적으로 변수라고 하면 결정론적 변수를 의미하므로 본 글에서는 결정론적 변수를 일반 변수라고 부르기로 한다.

그렇다면 확률론적 사건은 어떻게 표현할 수 있을까? 대표적인 확률론적 사건인 동전 던지기를 예로 들어 보자. 동전을 던지면 앞면 또는 뒷면이 랜덤하게 나온다. 편의상 앞면을 1, 뒷면을 0으로 표현하자. 그리고 동전 던지기의 결과값을 변수 $X$로 나타낸다고 하자. 이제 우리는 동전 던지기를 수학적으로 기술할 수 있게 되었다. 동전을 던졌을 때 “앞면이야, 뒷면이야?”라고 묻는 것을 “변수 $X$의 값이 뭐야?”라고 물어볼 수 있게 된 것이다. 이와 같이 불확실한 값을 표현하기 위하여 사용하는 변수를 확률변수(random variable)라고 한다. 확률변수를 이용하면 확률론적 현상을 수학적으로 기술할 수 있게 된다. 일반 변수와 마찬가지로 확률변수도 더하기, 곱하기 등 연산이 가능하다. 이에 대해서는 추후 자세히 살펴본다. 확률변수는 일반 변수 또는 샘플과 구분하기 위하여 통상 대문자로 표시한다.

그렇다면 질문 “변수 $X$의 값이 뭐야?”의 답은 무엇일까? “1일 수도 있고 0일 수도 있어”라고 답할 수도 있겠지만 우리는 수학적으로 표현하고 싶다. 확률변수의 값을 수학적으로 표현하는 방법은 나올 수 있는 모든 값과 그 값이 나올 확률을 함수로 표현하는 것이다. 동전 던지기의 경우 다음과 같은 함수를 사용할 수 있다.

\[f(x)=\begin{cases}\frac{1}{2},&\text{if $x=0$ or $1$}\\0,&\text{otherwise}\end{cases}\]

어려워 보이지만 아래 그림을 보면 쉽게 이해할 수 있다. $x$가 0 또는 1일 때만 1/2이며 그 외 모든 곳에서는 0인 함수이다.

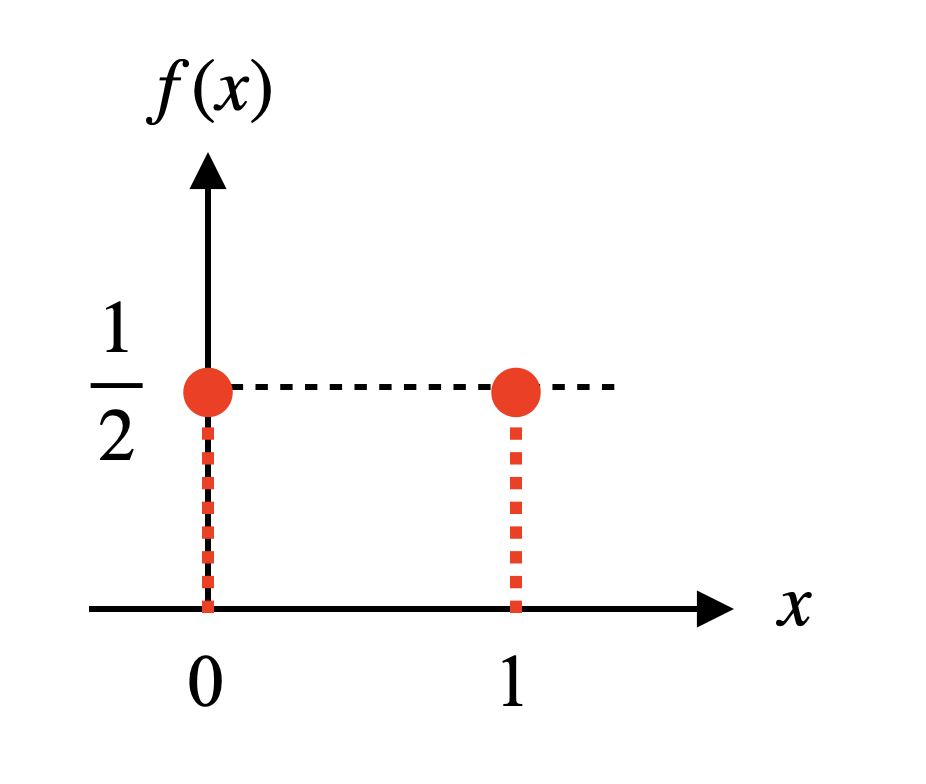
그림 1. 동전 던지기 확률분포

이렇게 확률변수의 값의 범위와 그 값이 나올 확률을 나타내는 함수를 확률분포(probability distribution)라고 한다.

확률변수 $X$의 값은 함수 $f(x)$로 표현되는 확률분포에 따라 정해지므로 $X$와 $f(x)$ 사이에는 연관관계가 있으며 이를 아래와 같이 물결무늬 기호를 이용하여 표현한다. 물결무늬 좌측에는 확률변수를 우측에는 그 확률변수의 확률분포를 나타낸다.

\[X\sim f(x)\]

함수 $f(x)$는 확률변수 $X$가 $x$일 때의 확률이므로 다음의 등식이 성립한다.

\[f(x)=P(X=x)\]

여기서 $P(\cdot)$은 괄호 안의 조건이 만족할 확률을 의미한다. 확률분포를 사용하면 마치 함수를 사용하는 것과 같이 확률을 구할 수 있다. 동전의 앞면이 나올 확률은 다음과 같이 얻을 수 있다.

\[f(1)=P(x=1)=0.5\]

이산 vs 연속

내일 낮 최고온도를 나타내는 확률변수를 $T$라고 하자. $T$가 14도일 확률이 가장 높지만 13.9도일 수도 있고 14.1도일 수도 있으며 확률은 낮지만 -5.6도일 수 있다고 가정하자. 이러한 확률분포를 표현하려면 연속적인 함수가 필요하다.

\[g(x)=\frac{1}{2\pi}e^{-(x-14)^2}\]

어려워 보이지만 그림으로 나타내면 아래와 같이 종 모양으로 표현된다.

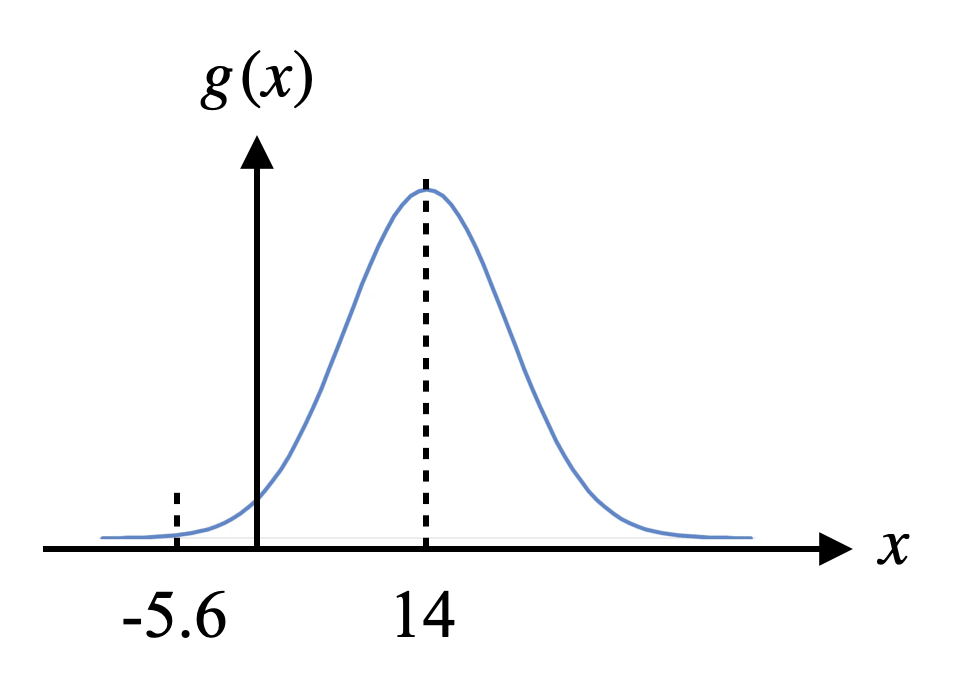
그림 2. 내일 낮 최고온도의 확률분포

확률변수 $T$는 확률분포 $g(x)$를 따르므로 다음과 같이 표현할 수 있다.

\[T\sim g(x)\]

$T$가 특정 값일 확률은 0이다. 예를들어 내일 낮 최고온도가 14도일 확률은 0이다.

\[P(T=14)=0\]

이상하게 들릴 수 있지만 수학의 연속 개념이 사용되었기 때문이다. 방바닥에 줄자를 늘어놓고 연필을 떨어뜨려 정확히 15 cm를 가리키는 지점에 맞출 확률이 0인 것과 같다고 이해하면 된다. 따라서 연속적인 확률분포인 경우 값의 범위를 지정해주어야 0보다 큰 확률이 나온다. 예를 들어 내일 낮 최고온도가 14도 이상일 확률은 아래와 같이 구한다.

\[\int_{14}^\infty g(x)dx=P(T\ge14)=0.5\]

동전 던지기의 $X$는 이산적인 현상을 표현하므로 이산확률변수(discrete random variable), 온도의 $T$는 연속적인 현상을 나타내므로 연속확률변수(continuous random variable)라고 한다. 또한 $f(x)$와 $g(x)$를 각각 확률질량함수(probability mass function, PMF)와 확률밀도함수*(probability density function, PDF)라고 한다.

* 적분을 해주어야 확률이 나오기 때문에 확률밀도(probability density)라고 한다.

확률변수의 이미지

일반 변수와 확률변수의 차이점을 이해하기 쉽도록 아래 그림의 이미지로 나타내었다.

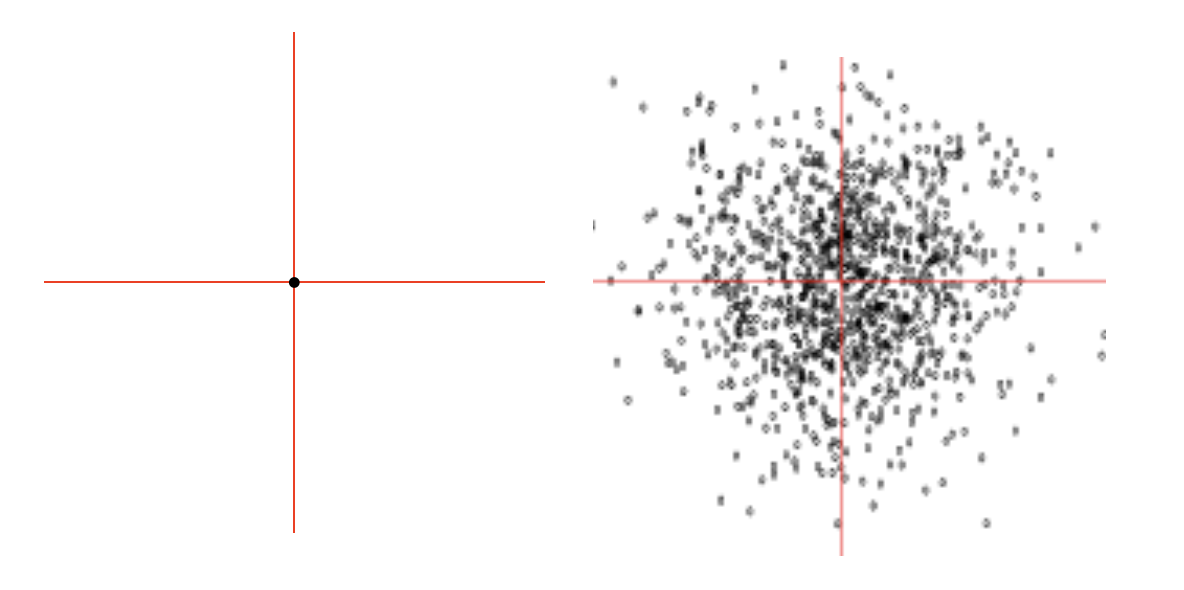
그림 3. 일반 변수와 확률변수의 이미지

상기 그림을 다트 게임의 결과라고 생각해도 좋다. 왼쪽 그림은 항상 정중앙에 맞추는 컴퓨터 시뮬레이션으로 생각하고 오른쪽 그림은 실력 좋은 선수가 실제로 던진 결과로 보면 좋을 것이다. 결정론적 변수의 값은 아무리 반복하더라도 같은 값이 나오지만 확률변수는 던질 때마다 다른 값이 나온다.

왜 확률분포를 사용하는가

결정론적 현상은 실재하지 않는데 우리는 왜 결정론적 변수와 수식을 주로 사용하는가? 확률변수와 확률분포를 사용하여 확률론적 현상을 기술하는 것이 상대적으로 어렵고, 복잡하기 때문이다. 하지만 세상을 제대로 설명하고 이해하려면 확률론적 관점이 반드시 필요하다.