확률과 통계는 무슨 차이가 있을까?

서양인의 사고방식으로 바라본 관점

개요

“확률과 통계” 또는 “확통”과 같이 우리는 흔히 확률과 통계를 묶어서 이야기한다. 이렇게 같이 붙어다니는 것을 보면 밀접한 관계가 있다는 것인데 확률과 통계는 같은 것일까? 아니라면 무슨 차이가 있는 것일까?
본 글에서는 확률과 통계가 무엇인지 그리고 어떤 차이가 있는 것인지 설명한다.

플라톤 vs 아리스토텔레스

아테네 학당 Wikipedia

잠시 그림을 보자. 모두가 아는 라파엘로의 “아테네 학당”이다. 그림에는 수 많은 위인들이 있지만 정중앙에는 두 사람이 나란히 서있다. 왼쪽 사람은 검지 손가락으로 하늘을 가리키고 있고 오른쪽 사람은 손바닥으로 땅을 가리키고 있다. 왼쪽은 플라톤, 오른쪽은 그의 제자인 아리스토텔레스이다.
플라톤은 이데아론을 제창한 것으로 유명하다. 원을 생각할 경우 현실에서 아무리 정확히 그린다 하더라도 완전하게 그릴 수 없다. 완전한 원은 오직 우리의 생각 속에만 존재한다. 플라톤은 말한다.

보편성은 특정한 것에서 멀리 떨어져 존재하며, 이는 그들의 원형(原型) 또는 전형이다.

반면 아리스토텔레스는 다음과 같이 말하였다.

철학적인 방법이란 특정한 현상에 대한 연구로부터 본질에 관한 지식에 이르기까지의 과정

플라톤의 이데아는 현실에는 존재하지 않는 이상적인 개념 또는 관념을 의미하며 현실은 이데아의 그림자일 뿐이라는 연역적인 세계관을 추구한다. 반면 아리스토텔레스는 현실로부터 출발하는 귀납적인 세계관을 추구한다.

서양인의 사고방식

서양인과 동양인의 사고방식 차이는 무엇일까? 서양인의 사고는 세계를 바라볼 때 두 가지 범주로 나누어 생각하는 이원론에 근간한다. 반면 동양인의 사고에는 세상의 모든 사물이 서로 연결되어 있다는 일원론에 입각한다. 서양의 이원론은 기원전 420년경에 살았던 플라톤의 사고에서 출발한다. 이원론의 시각으로 바라본 대상을 몇 가지만 나열해보자. 이데아와 현실, 선과 악, 천국과 지옥, 빛과 어둠, 이성과 감성, 마음과 몸, 부자와 빈자, 남자와 여자 등 무엇인가를 이해하기 위해서는 둘로 나누는 것부터 시작한다. 이원론적 세계관은 2천 년 가까이 서양인의 근원적인 사유 체계로 작동해왔다.[1]

이상과 현실

우리가 배우는 대부분의 학문은 서양으로부터 전해졌다. 따라서 학문의 근간을 이루고 있는 개념에도 이원론이 뿌리깊게 박혀있다. 잠시 전기회로이론을 생각해보자. 전류의 흐름을 방해하는 장치를 저항이라고 하며 아래의 전기회로도에서 $R$로 표시한 기호로 나타낸다. 회로도에서 직선은 이상적인 전선을 의미하며 저항이 0 $\Omega$이다.

link

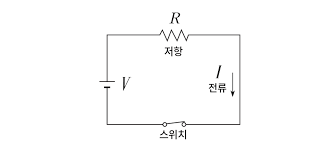
하지만 현실의 전기회로에는 모든 것이 저항이다. 단지 전류를 방해하는 정도의 차이가 있을 뿐이다.

link

공대생 또는 엔지니어들은 전기회로도를 모델(model) 또는 수학적 모델(mathematical model)이라고 부른다. 복잡한 현실을 단순화하여 이론적으로 다룰 수 있도록 하는 방법이다. 전기회로이론 뿐만 아니라 모든 학문(공학, 물리학, 경제학, 사회학 등)에는 수학적 모델을 이용하여 현실을 이해하려고 노력한다. 모델은 이상이고 실제 물체 또는 현상은 현실이다. 이와 같이 서양의 학문은 플라톤의 이상과 아리스토텔레스의 현실로 분리하는 이원론에 근간한다.

몇 가지 분야에서 발견할 수 있는 이상과 현실을 살펴보자.

Area	Ideal	Real
engineering	system model	observed data (experimental data)
computer science	type, class	variable, constant, object
	declaration	definition
English	cow	a cow, the cow

확률과 통계

여기까지 왔으면 드디어 확률과 통계를 이해할 준비가 되었다. 결론부터 말하겠다.

확률은 이상이고 통계는 현실이다.

예를 들어보자. 동전의 앞뒤면이 나올 확률이 각각 1/2이라는 것의 진정한 의미가 무엇인가? 통계학자 중 빈도주의자(frequentist)의 견해에 따르면 동전을 무한히 던졌을 때 앞뒤면이 나올 비율이 각각 50%라는 의미이다. 하지만 동전을 무한히 던질 수 있을까? 불가능하다. 결국 동전 앞면이 나올 확률 1/2이라는 것은 이 세상 누구도 확인할 수 없는 이상 세계에서만 존재하는 관념인 것이다. 플라톤의 원(circle)과 마찬가지 개념이다.
통계는 무엇인가? 우리가 실험을 하면 데이터를 얻을 수 있다. 동전의 앞면을 1, 뒷면을 0이라고 하자. 동전을 10번 던져서 아래와 같은 데이터를 얻었다고 가정하자.

0 1 1 0 1 1 1 0 0 1

이로부터 우리는 다음 번에 앞뒤면이 나올 가능성을 예측(계산)할 수 있다. 각각 0.6와 0.4이다. 이상적인 1/2과는 다른 값을 얻는다. 물론 5번씩 앞뒤면이 나왔다면 이상적인 확률과 일치하지만 한 번만 더 던지면 다시 달라진다. 이와 같이 통계는 현실 데이터를 세거나(하나, 둘, …) 계산하는 방법으로 “관심있는 정보”를 얻는 과정을 다룬다. 여기서 “관심있는 정보”에 주의를 기울여보자.

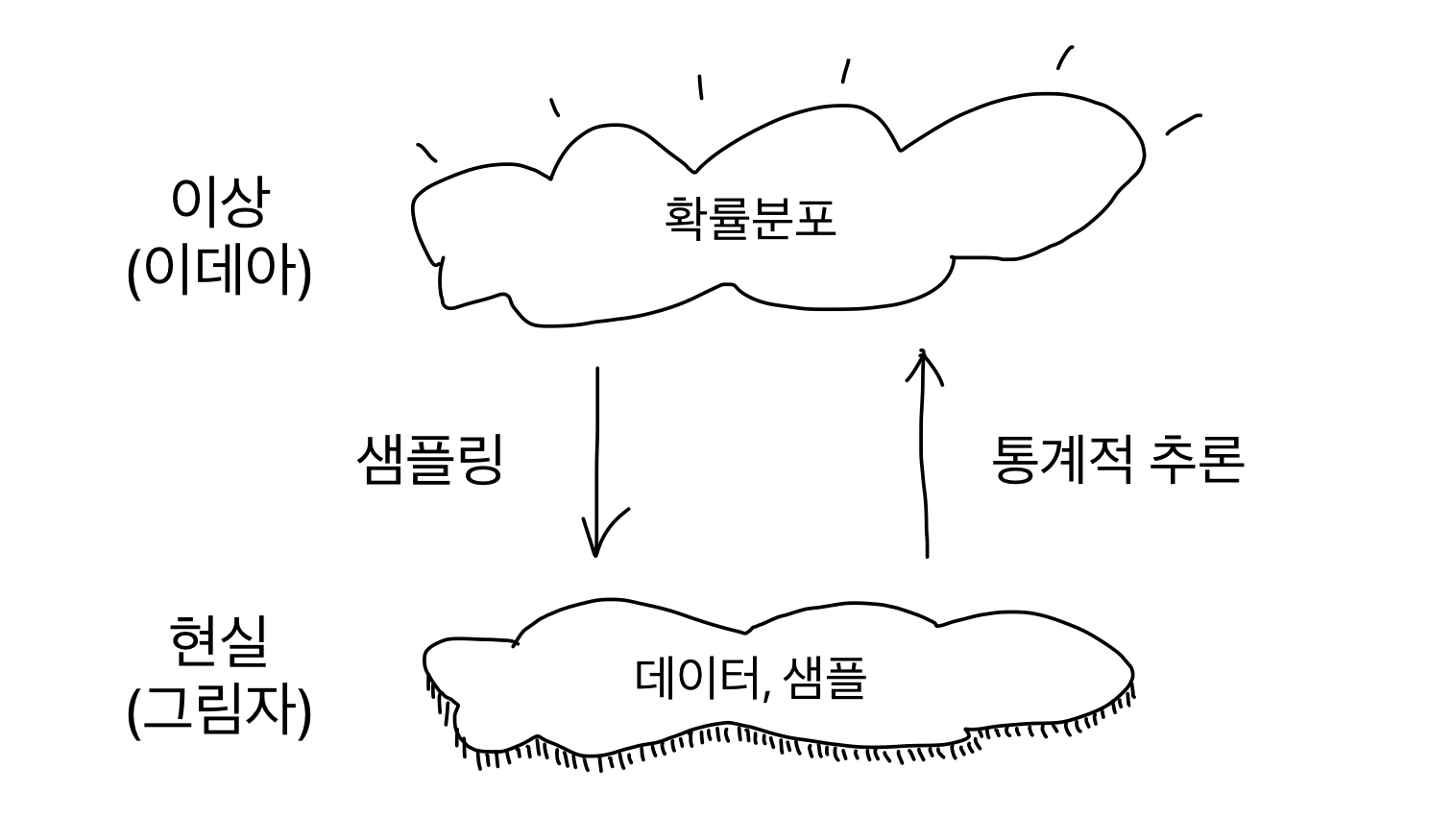
샘플링 vs 통계적 추론

확률통계학에서 동전을 던지는 행위를 실험(experiment)이라고 한다. 실험을 통하여 우리는 데이터를 얻는다. 이렇게 얻은 데이터를 샘플(sample)이라고 하며 샘플을 얻는 행위를 샘플링(sampling)이라고 부른다. [2] 샘플링(또는 실험)은 (우리가 알 던 모르던) 동전 앞뒤가 나올 확률로부터 데이터를 생성하는 과정이다. 이상적인 확률로부터 현실적인 데이터를 추출한다.

반대로 데이터로부터 확률을 구하는 과정이 있을까? 있다. 이를 통계적 추론(statistical inference)이라고 한다. 동전을 던져서 얻은 데이터로부터 앞뒤면이 나올 확률을 구하거나 전교생의 수학성적으로부터 평균을 구하는 과정이 통계적 추론의 예이다.

미리 보기

앞으로 확률과 통계를 배우면서 가끔 아래 표를 보고 내가 어디까지 왔는지 확인해보면 재미있을 것이다.

Ideal	Real
probability	statistics
random variable probability distribution	sample
model parameter (ex: expectation, variance) [4]	statistic [3] or estimate

주석

[1] 「지적 대화를 위한 넓고 얕은 지식 제로 : 지혜를 찾아 138억 년을 달리는 시간 여행서」 채사장, 웨일북, 2019.
[2] 참고로 컴퓨터공학에서 type, class로부터 variable, constant, object를 메모리에 생성하는 과정을 인스턴스화(instantiation)라고 하며 생성된 객체를 인스턴스(instance)라고 한다.
[3] 참고로 statistics는 통계학, statistic은 샘플 데이터로부터 계산한 값(또는 식)을 의미한다. 전혀 다른 뜻이므로 주의해야 한다.
[4] 위에서 말한 “관심있는 정보”란 probability distribution의 parameter 또는 model parameter를 의미한다.

References

1. 「지적 대화를 위한 넓고 얕은 지식 제로 : 지혜를 찾아 138억 년을 달리는 시간 여행서」 채사장, 웨일북, 2019.