차원해석(dimensional analysis)이란 무엇인가

학교에서 유체역학 수업을 들을 때였다. 교수님께서 네비어-스톡스 방정식(Navier-Stokes equation)을 적고 계셨다.

\[\frac{\partial u_i}{\partial t}+u_k\frac{\partial u_i}{\partial x_k}=-\frac{\partial p}{\partial x_i}+\cdots\]

그런데 아무리 확인해봐도 좌변과 우변의 차원(dimension)이 맞지 않았다. $u$는 유속(flow velocity), $t$는 시간, $p$는 압력, $x$는 변위를 의미하므로 좌변의 차원은 속도/시간 (첫 번째 항) 또는 속도×속도/변위 (두 번째 항)이므로 가속도 차원이 되고, 우변은 압력/변위 = (힘/면적)/변위 = 힘/(면적×변위) = 힘/부피 이므로 단위 부피 당 힘이 된다. 좌변에 밀도가 곱해지면 우변과 차원이 같아지게 된다는 생각에 교수님께 “좌변에 밀도가 빠진 것 같은데요”라고 했더니 “그러네” 하시면서 밀도 $\rho$를 추가하셨던 적이 있다.

\[\rho \left(\frac{\partial u_i}{\partial t}+u_k\frac{\partial u_i}{\partial x_k}\right)=-\frac{\partial p}{\partial x_i}+\cdots\]

이와 같이 방정식이 올바른지 확인할 수 있으며 심지어 오류를 수정할 수도 있는 차원해석(dimensional analysis)에 대해 알아보자.

---

이전 글에서 7가지 기본단위와 그 조합으로 모든 물리량을 나타낼 수 있다고 하였다. 기본단위를 조합하여 만든 단위를 유도단위(derived units)라고 한다. 여기서 조합이란 곱하거나 나누는 것을 의미한다. 미분과 적분도 각각 나누기와 곱하기로 볼 수 있다.

\[v=\frac{ds}{dt}=\lim _{\Delta t\rightarrow 0}^{ }\frac{s(t+\Delta t)-s(t)}{\Delta t}\] \[q=\int _{t_0}^{t_1}i\ dt=\lim _{\Delta t\rightarrow 0}^{ }\left[i\left(t_0+\frac{\Delta t}{2}\right)\Delta t+i\left(t_0+3\frac{\Delta t}{2}\right)\Delta t+\cdots \right]\]

모든 물리량에는 차원(dimension)이 존재한다. 차원은 기본단위를 어떻게 조합하였는지를 나타내며 기본물리차원의 지수형태로 표현할 수 있다. 기본물리차원은 다음 표와 같다.
​

표 1. 기본물리차원

차원	기호	기본단위
시간(time)	T	s
길이(length)	L	m
질량(mass)	M	kg
전류(electric current)	I	A
온도(temperature)	$\Theta$	K
물질량(amount of substance)	N	mol
광도(luminous intensity)	J	cd

예를 들어, 1 시간, 24 초, 100 ms는 모두 시간을 나타내며 차원은 T이다. 1 kg, 100 g은 질량을 나타내며 차원은 M이다.

유도단위의 차원을 기본물리차원의 지수형태로 표현할 수 있으며 몇 가지 예로 설명하면 다음과 같다.

• 속도는 거리를 시간으로 나눈 값이므로 L/T = T$^{-1}$L 차원이다. m/s, km/h, cm/min의 차원은 모두 T$^{-1}$L이다.
• 가속도는 속도를 시간으로 나눈 값이며 차원은 T$^{-2}$L이다. m/s$^2$의 차원은 T$^{-2}$L이다.
• 힘은 뉴턴 법칙 F=ma에 의하여 가속도와 질량을 곱한 값이다. 따라서, 힘의 차원은 T$^{-2}$LM이다. N (= kg·m/s$^2$), kgf ($\approx$ 9.81 N)의 차원은 모두 T$^{-2}$LM이다.

일반적으로 모든 물리량의 차원은 다음과 같이 7개의 지수로 나타낼 수 있다.

dim Q = T$^a$ L$^b$ M$^c$ I$^d$ $\Theta^e$ N$^f$ J$^g$

프로그래밍 언어로 표현한다면 배열(array)이나 튜플(tuple)로 지수만 저장하면 될 것이다.

(a, b, c, d, e, f, g)

시간의 차원 T는 T$^1$L$^0$M$^0$I$^0$$\Theta^0$N$^0$J$^0$과 같으므로

(1, 0, 0, 0, 0, 0, 0),

속도의 차원 T$^{-1}$L은

(-1, 1, 0, 0, 0, 0, 0),

힘의 차원 T$^{-2}$LM은

(-2, 1, 1, 0, 0, 0, 0)

과 같이 나타낼 수 있다.

자주 사용하는 물리량의 차원을 다음의 표에 나타내었다.

표 2. 자주 사용하는 물리량의 차원

물리량	단위 예	차원 (T, L, M, I, $\Theta$, N, J)	비고
속도	m/s, kph	(-1, 1, 0, 0, 0, 0, 0)	거리 / 시간
가속도	m/s$^2$	(-2, 1, 0, 0, 0, 0, 0)	속도 / 시간
힘	N, kgf	(-2, 1, 1, 0, 0, 0, 0)	가속도 × 질량
일, 에너지	J (Joule)	(-2, 2, 1, 0, 0, 0, 0)	힘 × 거리
동력(파워)	W, kW	(-3, 2, 1, 0, 0, 0, 0)	일 / 시간
전압	V, mV	(-3, 2, 1, -1, 0, 0, 0)	파워 / 전류
전하량	C (Coulomb)	(1, 0, 0, 1, 0, 0, 0)	전류 × 시간
캐패시티	F, $\mu$F	(4, -2, -1, 2, 0, 0, 0)	전하량 / 전압

그렇다면 물리량의 차원은 왜 알아야 하는가? 물리량의 기본차원을 식별하여 서로 다른 물리량의 관계를 분석하는 데에 활용되며 이러한 작업을 차원해석(dimensional analysis)이라고 한다. 차원해석을 잘 활용하면 물리식의 오류를 발견하거나 심지어 올바른 식을 예측할 수도 있다.

차원해석의 활용법은 다양하지만 본 글에서는 매우 유용한 몇 가지만 설명하고자 한다.

(1) 두 물리량을 비교할 때에는 차원이 동일해야 한다.
(2) 두 물리량을 더하거나 뺄 때에는 차원이 동일해야 한다.
(3) sin, exp 등 초월함수의 인자는 무차원이어야 한다.
(4) 보이지 않는 차원이 존재할 수 있음을 주의해야 한다.

하나씩 자세히 살펴보자.
​

(1) 두 물리량을 비교할 때에는 차원이 동일해야 한다

다음 문장을 보고 물리학의 관점으로 볼 때 맞는 문장인가 생각해보자.

1. 네 키가 내 몸무게보다 더 크네.
2. 이 택배는 무게가 많이 나가네. 12 kg이나 해.
3. 저 차는 속도가 엄청 빠르다. 제로백이 3 초 밖에 안해.

1번 문장은 누가 보더라도 틀린 문장인 것을 알 수 있다. 키와 몸무게를 비교하는 것이 말이 되는가?
2번과 3번 문장은 일상적인 대화로는 문제가 없지만 물리학적으로는 둘 다 틀린 문장이다.

2번 문장에서 무게(weight)는 하중, 중량과 같이 힘을 나타내는 개념이지만 12 kg은 질량을 나타낸다. 질량이 12 kg인 물체가 지표면에 있을 때 작용하는 하중, 즉, 무게는 12 kgf 또는 약 120 N으로 표현해야 한다.

3번 문장에서 제로백은 자동차가 정지상태에서 100 kph에 도달할 때까지 걸리는 시간으로써 가속도를 나타내는 개념이다. 따라서 “가속도가 엄청 크다” 또는 “힘이 매우 세다”라고 해야 물리적으로 맞는 표현이 된다. (가속도에 질량을 곱하면 힘이므로 질량이 크게 변하지 않는 물체의 가속도와 힘은 서로 상응하는 물리량으로 볼 수 있다.)

이와 같이 우리는 일상 속에서 차원이 다른 두 물리량을 “같다”, “크다”, “작다” 등의 표현으로 비교하기도 한다. 하지만 학술적으로는 명백한 오류이다. 키(길이)와 몸무게(질량 또는 힘) 뿐만 아니라 속도와 가속도를 비교하거나 질량과 힘을 비교하는 것은 불가능하다.

다음 식은 진자의 주기를 구하는 방정식이다. $T$는 주기(시간), $\ell$은 진자의 길이, $g$는 중력가속도이다. 물결무늬 기호는 근사치를 의미한다. 여기서는 그냥 등식으로 생각해도 무방하다.

\[T\approx 2\pi \sqrt{\frac{\ell}{g}}\]

좌변은 시간이므로 차원이 T이다. 그렇다면 우변도 차원이 T이어야 한다. 2$\pi$는 상수이므로 차원이 없다. 무차원이다. $\ell$은 길이이므로 차원이 L이다. $g$는 중력가속도이므로 가속도 차원이며 T$^{-2}$L이다. $\ell$/g의 차원은 L / T$^{-2}$L = T$^2$가 된다. 여기에 제곱근을 하면 차원이 T가 된다. 결국, 좌변의 차원과 같아진다.

하나만 더 보자. 유명한 아인슈타인의 에너지-질량 등가 공식이다.

\[E=mc^2\]

좌변은 에너지이므로 차원이 T$^{-2}$L$^2$M이다. 우변은 질량 곱하기 빛의 속도의 제곱이므로 M(T$^{-1}$L)$^2$ = T$^{-2}$L$^2$M 차원이 되며 좌변의 차원과 같다.

이와 같이 차원해석을 이용하면 복잡한 방정식이 어떤 의미인지, 등식이 성립하는지 등을 파악할 수 있다.
​

(2) 두 물리량을 더하거나 뺄 때에는 차원이 동일해야 한다

비교할 때와 마찬가지로 서로 다른 차원의 물리량을 더하거나 빼는 것은 불가능하다. 예를 들어, 아래 식과 같이 길이와 속도를 더하는 것은 물리적으로 불가능하다.

100 m + 25 kph = ?

곱으로(나눗셈 포함) 이루어진 항(term)을 더할 때도 각 항의 차원이 일치해야 한다. 아래의 라그랑주 방정식(Lagrange’s equation)을 살펴보자.

\[\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_j}\right)-\frac{\partial L}{\partial q_j}=0\]

두 번째 항이 좀 더 단순하므로 먼저 분석해보면 L은 라그랑지안(Lagrangian)으로 운동 에너지에서 위치 에너지를 뺀 값이다. 결국 에너지이므로 차원은 T$^{-2}$L$^2$M이다. $q$는 일반화된 좌표(generalized coordinates)로서 여기서는 변위로 생각하자.(각도 등 다른 물리량이더라도 결과는 같다.) 미분도 나누기로 생각할 수 있으므로 에너지를 변위로 나누면 (T$^{-2}$L$^2$M)/L = T$^{-2}$LM 차원이 되며 이는 힘의 차원과 같다. 즉, 라그랑주 방정식의 두 번째 항은 결국 힘을 의미한다.
첫 번째 항의 차원을 분석해보자. 괄호 밖의 미분은 시간으로 나누는 것과 같으며 $q$ 위의 점(dot)도 시간으로 미분하는 것을 의미한다. 따라서 [에너지 / (변위 / 시간)] / 시간이므로 (T$^{-2}$L$^2$M) / (L/T) / T = T$^{-2}$LM 차원이 되어 결국 힘의 차원이 된다. 첫 번째 항과 두 번째 항은 모두 힘의 차원이므로 서로 더하거나 뺄 수 있다.

앞에서 소개한 네비어-스톡스 방정식은 각 항의 차원이 모두 단위 부피 당 힘, 즉, T$^{-2}$L$^{-2}$M이다.
​

(3) 초월함수의 인자는 무차원이어야 한다

초월함수(transcendental function)란 다항식의 근으로 정의할 수 없는 함수를 말한다. sin, cos, tan, exp, log 함수가 대표적인 예이다. 초월함수는 테일러 급수(Taylor series)로 전개하면 무한히 많은 항으로 표현된다. 예를 들어 sin과 exp 함수는 다음과 같이 표현된다.

\[\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots\] \[\exp x=e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots\]

테일러 급수를 보면 각 항의 지수가 모두 다르다. 만약 함수 인자에 단위가 있다면 어떻게 될까? 각 항의 차원이 모두 달라질 것이다. 예를 들어 인자의 차원이 길이라고 한다면 1차항은 길이, 2차항은 면적, 3차항은 부피 차원이 될 것이다. 이는 “(2) 두 물리량을 더하거나 뺄 때에는 차원이 동일해야 한다”를 위배한다. 따라서 초월함수의 인자는 단위가 없는 무차원(dimensionless)이어야 한다.

---

그렇다면 우리가 그동안 사용해온 sin(30$^\circ$)와 같이 각도는 차원이 없단 말인가? 결론부터 말하자면 각도는 무차원이다. 차근차근 알아보자.

흔히 사용하는 각도 단위로 $^\circ$(degree, 도)와 rad(radian, 라디안)이 있다. $^\circ$는 일상생활에서 많이 쓰는 단위로 원 둘레를 한 바퀴 도는 각도를 360$^\circ$로 정의하여 사용한다. 라디안은 원호(부채꼴, arc)에 대해서 호의 길이를 반지름으로 나눈값이다. 호의 길이 대 반지름의 비(ratio)로 생각해도 된다. 왜 반지름으로 나눈 비(ratio)를 사용할까? 각도가 동일한 호라면 호의 크기(또는 반지름)에 상관없이 비는 일정하기 떄문이다. 라디안을 만든 사람은 머리가 좋다고 생각되지 않는가? 두 길이의 비를 이용하여 각도를 나타내는 방법을 고안한 것이다.

완전한 원을 생각해보면 호의 길이는 원둘레와 같아지므로 $2\pi r$이 된다. 이를 반지름으로 나누면 $2\pi$이므로 360$^\circ$ = $2\pi$ rad임을 알 수 있다. 양변을 2로 나누면 반원일 때의 관계식을 얻을 수 있다.

180$^\circ$ = $\pi$ rad$\tag{1}$

이 관계식은 반드시 암기하도록 하자. 식 (1)의 양변을 2 또는 3으로 나누면 90$^\circ$ = $\pi$/2 rad, 60$^\circ$ = $\pi$/3 rad도 얻을 수 있다. 식 (1)을 $\pi$로 나누면 1 rad = (180/$\pi$)$^\circ$ $\approx$ 57.295$^\circ$임을 알 수 있다.

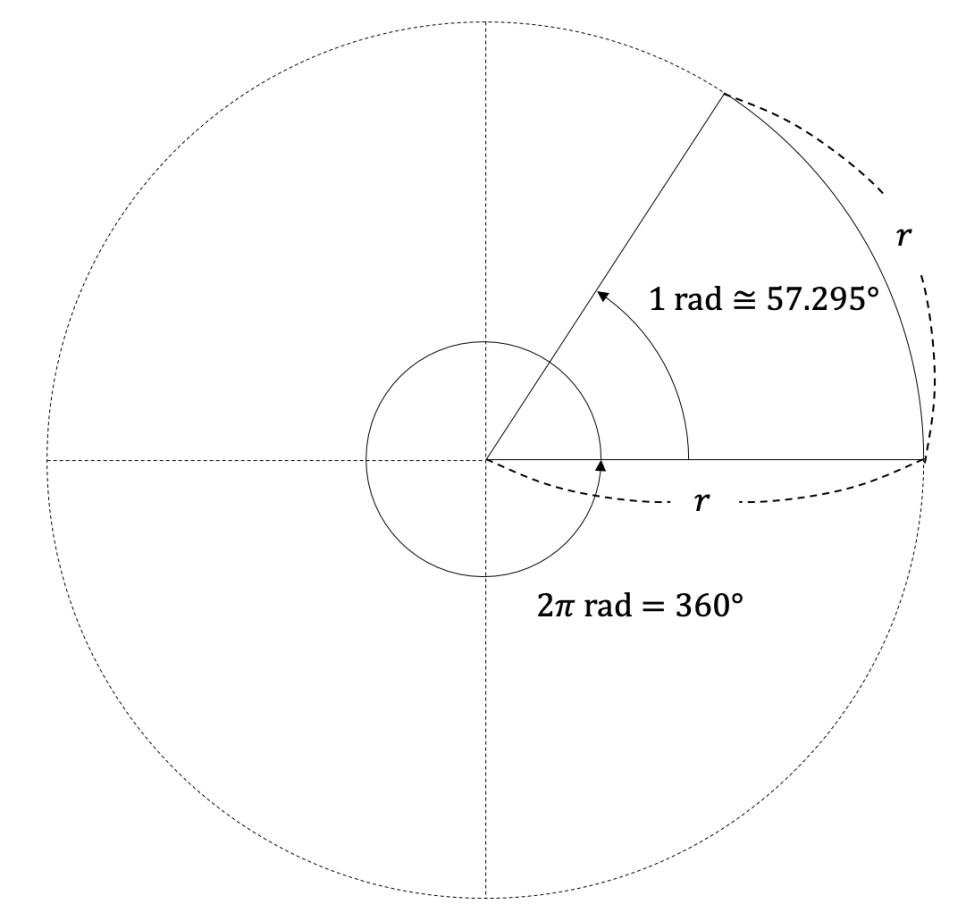
라디안의 정의

잠깐 옆길로 샌 것 같지만 각도가 왜 무차원인지 이미 설명을 마쳤다. 어디서? 앞에서 라디안은 호의 길이를 반지름으로 나눈값, 즉, 두 길이의 비를 이용하여 각도를 나타내는 방법이라고 하였다. 만약 반지름이 1 m인 반원의 경우 각도를 라디안으로 표현하면 ($\pi$ m)/(1 m) = $\pi$ rad이 된다. 즉, rad = m/m = cm/cm = km/km인 셈이다. 라디안은 무차원이므로 rad을 붙이지 않아도 라디안으로 생각할 수 있다. 예를 들면 다음과 같이 쓸 수 있다.

sin($\pi$ rad) = sin($\pi$)

그렇다면 $^\circ$도 무차원인가? 그렇다. 같은 각도를 다르게 표현한 것이므로 무차원이다. 단, 반드시 단위 $^\circ$를 붙여주거나 라디안으로 변환하여야 한다. 만약 사인 30도를 표현하려면 아래의 첫 번째 줄처럼 쓰면 안된다.

sin(30) ($\times$)
sin(30$^\circ$) ($\checkmark$)
sin($\pi$/6) ($\checkmark$)
​

(4) 보이지 않는 차원이 존재할 수 있음을 주의해야 한다

드디어 마지막 항목만 남았다. 물리시간에 파동을 배우고 있다고 생각해보자. 한 점에서의 파동의 변위를 $y$, 파동의 주파수를 $f$, 시간을 $t$라고 한다면 아래와 같이 표시할 수 있다.

\[y=\sin (2\pi ft)\]

여기서 $f$는 Hz 단위이며 $t$는 초 단위이다. Hz = 1/s이므로 sin 함수의 인자는 무차원이 된다. 좌변의 $y$가 길이 차원인데 우변도 길이 차원이어야 하지 않는가? 이런 경우에는 다음과 같이 생략된 부분이 있다고 봐야 한다.

\[y=1\cdot \sin (2\pi ft)\]

sin 함수 앞에 진폭 1 m가 생략된 것이다.