강화학습: 가치함수법(Value function methods)

최적정책을 찾는 방법은 크게 최적가치함수(optimal value function) 를 찾은 후 최적정책을 구하는 가치함수법(value function methods) 과 직접 최적정책을 찾는 정책경사법(policy-gradient method) 으로 구분할 수 있다. 본 장에서는 가치함수법 중 비교적 작은 크기의 환경(small-scale environment)을 풀 때 사용할 수 있는 고전적인 강화학습을 살펴본다.

1. DP, MC, and TD

최적가치함수를 찾는 방법은 크게 동적계획법(Dynamic Programming, DP), 몬테카를로 방법(Monte Carlo Method, MC) 과 시간차학습(Temporal-Difference Learning, TD) 으로 나눌 수 있다.

DP는 I.4. Value function에서 설명한 벨만방정식을 이용하는 방법이다. 현재 상태(또는 현재 상태-행동)에서 한 스텝 후에 도달할 수 있는 모든 상태(또는 상태-행동)의 가치를 이용하여 현재 상태가치(또는 행동가치)를 업데이트하는 방법이다.

MC는 주어진 정책에 따라 현재 상태에서부터 종료상태까지 반복적으로 진행하여 얻은 이득으로 현재 가치를 업데이트하는 방법이다.

TD는 행동을 수행하고 한 스텝 후에 도달한 다음 상태의 가치와 이 때 받은 보상을 더한 값으로 현재 가치를 업데이트하는 방법이다.

DP는 한 스텝 후에 도달할 수 있는 모든 가치의 완전한 분포에 기반하여 현재 가치를 업데이트하는 기대값 업데이트(expected update) 를 사용한다. 반면 MC와 TD는 경로 샘플 또는 스텝 샘플을 이용하여 현재 가치를 업데이트하는 샘플 업데이트(sample update) 를 사용한다. 기대값 업데이트는 이미 분포를 알고 있으므로 반복적인 샘플링이 불필요하지만¹ 환경모델을 알아야 한다는 단점이 있다.

MC와 TD는 가치함수의 목표치(target) $U_t$와 추정치(estimate) $V_\pi(s_t)$의 차이에 학습률(learning rate) $\alpha$를 곱한 값을 현재 가치에 더하는 방식으로 현재 가치를 업데이트한다. 즉, 현재 가치함수의 추정치를 목표치에 근접시키는 과정을 반복한다.

\[V_\pi(s_t)\leftarrow V_\pi(s_t) + \alpha[U_t - V_\pi(s_t)]\tag{1}\]

가치함수 목표치 $U_t$의 엄밀한 값은 현재 상태 $s_t$에서 받을 수 있는 이득의 기대값(expected return)이다.

\[\begin{aligned} U_t&=\mathbb{E}\left[G_t\right] \\ &=\mathbb{E}\left[\sum_{k=0}^\infty \gamma^k R_{t+k+1}\right] \\ &=\lim\limits_{N\rightarrow\infty}\frac{1}{N}\sum_{n=1}^N\left[\sum_{k=0}^\infty \gamma^k R_{t+k+1}\right] \end{aligned}\]

기대값은 무한히 반복한 후 평균을 낸 값이다. 하지만 실제로 무한히 반복하여 평균을 낼 수는 없기 때문에 추정량(estimator)을 이용하여 기대값을 추정한다.²

MC에서는 목표치 $U_t$에 대한 추정량이 이득 $G_t$이고, TD에서는 보상과 할인된 다음 상태가치를 더한 값 $R_{t+1} + \gamma V_\pi(S_{t+1})$이다.

\[V_\pi(s_t)\leftarrow V_\pi(s_t) + \alpha[G_t - V_\pi(s_t)]\tag{MC}\] \[V_\pi(s_t)\leftarrow V_\pi(s_t) + \alpha[R_{t+1} + \gamma V_\pi(S_{t+1}) - V_\pi(s_t)]\tag{TD}\]

Figure 1은 퇴근 중 집에 도착하는 시간을 예측하는 예를 들어 MC와 TD의 차이점을 설명하는 그림{Sutton.2018}(123p)이다. 좌측의 MC 방법은 실제로 집에 도착한 시간으로 중간 예측을 업데이트하고 우측의 TD는 다음 스텝의 예측으로 이전 스텝의 예측을 업데이트한다.

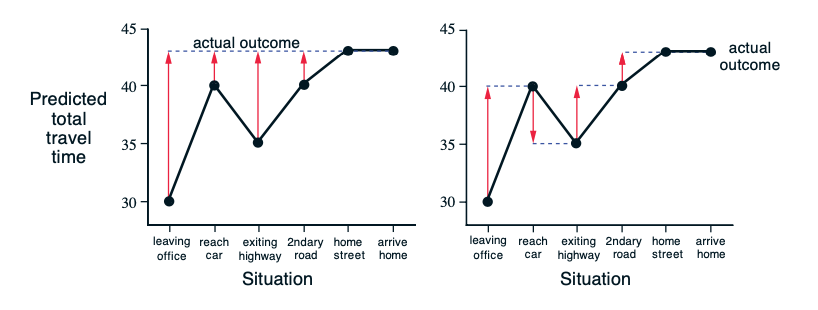
Figure 1. Monte Carlo methods vs. temporal-difference learning

Figure 2에 도시한 바와 같이 MC는 종료상태까지 진행해야 업데이트가 가능하지만 DP와 TD는 한 스텝만 진행해도 업데이트가 가능하다. DP와 TD는 추정치로 추정치를 업데이트하기 때문이며 이러한 방법을 부트스트랩(bootstrap) 이라고 한다.

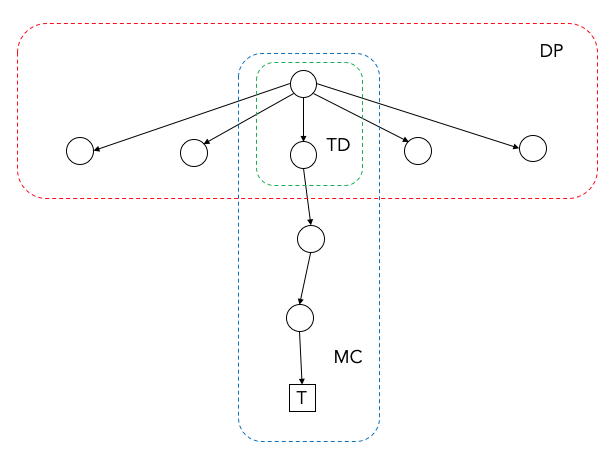
Figure 2. DP, MC and TD

추정량을 사용할 떄는 편향(bias)³과 분산(variance)을 고려해야 한다. MC의 목표치는 불편추정량(unbiased estimator)이지만 TD의 목표치는 편의추정량(biased estimator)이다.⁴ 반면 MC의 목표치는 분산(variance)이 크지만 TD의 목표치는 분산이 적다.⁵ 이러한 특징을 Table 1에 나타내었다.

Table 1. MC vs. TD

	MC	TD
Estimator	$G_t$	$R_{t+1}+\gamma V(S_{t+1})$
Bias	0	> 0
Variance	High	Low

Table 2에 DP, MC, TD의 특징을 정리하였다. 실제 강화학습에는 모델이 필요하지 않으면서 한 스텝 샘플로 업데이트가 가능한 TD 방법이 가장 많이 쓰인다.

Table 2. DP, MC, TD

	DP	TD	MC
model-based	O	X	X
sample update	X	O	O
bootstrap	O	O	X

2. Temporal-difference methods

본 절에서는 중요한 TD 알고리즘 몇 가지를 살펴본다.

가장 기본적인 TD 알고리즘인 TD(0)는 앞에서 설명한 바와 같이 한 스텝 후의 보상에 다음 상태의 가치를 더한 값을 목표치로 사용한다.

\[V_\pi(s_t)\leftarrow V_\pi(s_t) + \alpha[R_{t+1} + \gamma V_\pi(S_{t+1}) - V_\pi(s_t)]\]

TD(0)의 행동가치함수 버전이 Sarsa 알고리즘이다. Sarsa는 state-action-reward-state-action의 조합으로 만든 용어이다.

\[Q_\pi(s_t,a_t)\leftarrow Q_\pi(s_t,a_t) + \alpha[R_{t+1} + \gamma Q_\pi(S_{t+1},A_{t+1}) - Q_\pi(s_t,a_t)]\]

Q-learning은 Sarsa의 다음 행동가치 샘플 $Q_\pi(S_{t+1},A_{t+1})$ 대신 최대값 $\max\limits_{a\in A_{t+1}}Q_\pi(S_{t+1},a)$을 사용하는 알고리즘이다.

\[Q_\pi(s_t,a_t)\leftarrow Q_\pi(s_t,a_t) + \alpha[R_{t+1} + \gamma \max\limits_{a\in A_{t+1}}Q_\pi(S_{t+1},a) - Q_\pi(s_t,a_t)]\]

세 알고리즘의 추정량을 Table 3에 정리하였다.

Table 3. Estimator of TD(0), Sarsa, and Q-learning

	Value estimated	TD target
TD(0)	$v_\pi(s_t)$	$R_{t+1} + \gamma V_\pi(S_{t+1})$
Sarsa	$q_\pi(s_t,a_t)$	$R_{t+1} + \gamma Q_\pi(S_{t+1},A_{t+1})$
Q-learning	$q_\pi(s_t,a_t)$	$R_{t+1} + \gamma \max\limits_{a\in A_{t+1}}Q_\pi(S_{t+1},a)$

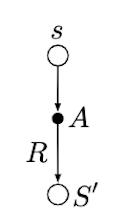
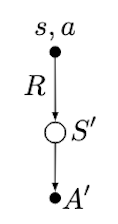
백업다이어그램으로 비교하면 Figure 3과 같다.

TD(0)	Sarsa	Q-learning

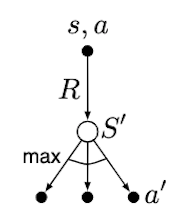Figure 3. Backup diagrams of TD(0), Sarsa, and Q-learning

3. Function approximation

상태공간의 크기가 비교적 작은 MDP를 풀 때는 상태가치함수 또는 행동가치함수를 테이블 형태로 만들어 업데이트를 하면 최적가치함수를 찾을 수 있고 이로부터 최적정책을 만들 수 있다. 하지만 바둑, 큐브퍼즐(Rubik’s cube)이나 자율주행을 위한 영상신호, 7자유도 로봇팔의 관절운동과 같이 상태공간이 매우 크거나 연속상태공간을 다룰 때에는 함수근사화(function approximation) 기법이 필요하다.

상태가치함수 $v_\pi(s_t)$를 근사하기 위한 함수(function approximator)를 $\hat{v}(s_t,\mathbf{w_t})$라고 한다면 평균제곱가치오차(mean squared value error) $\overline{VE}$는 다음과 같이 정의된다.

\[\begin{aligned} \overline{VE}(\mathbf{w})&\doteq\sum\limits_{s\in S}\rho(s)\left[v_\pi(s)-\hat{v}(s,\mathbf{w})\right]^2 \\ &=\mathbb{E}_\rho\left[\left[v_\pi(s)-\hat{v}(s,\mathbf{w})\right]^2\right] \end{aligned}\]

여기서 $\rho(s)$는 정상상태 분포이고 $\mathbb{E}_\rho[\cdot]$은 $\rho(s)$에 대한 기대값을 의미한다.

최적의 근사함수를 얻기 위해서는 $\overline{VE}(\mathbf{w})$를 최소화하는 파라미터 $\mathbf{w}$를 찾아야 한다. 이를 위하여 경사하강법(gradient-descent method)을 고려할 수 있다. 경사를 구하기 위하여 $\nabla_{\mathbf{w}}\overline{VE}(\mathbf{w})$를 계산하여야 하지만 정상상태분포를 구하기 위해서 수많은 에피소드가 필요하기 때문에 현실적이지 못하다. 이를 극복하기 위하여 확률론적 경사하강법(stochastic gradient-descent, SGD)을 사용할 수 있다. SGD는 $\nabla_{\mathbf{w}}\overline{VE}(\mathbf{w})$의 샘플인 $\nabla_{\mathbf{w}}\left[v_\pi(s)-\hat{v}(s,\mathbf{w})\right]^2$을 이용하여 최적화를 수행하는 방법이다.

\[\begin{aligned} \mathbf{w_{t+1}}&=\mathbf{w_t}-\frac{1}{2}\alpha\nabla_{\mathbf{w}}\left[v_\pi(s_t)-\hat{v}(s_t,\mathbf{w_t})\right]^2 \\ &=\mathbf{w_t}+\alpha\left[v_\pi(s_t)-\hat{v}(s_t,\mathbf{w_t})\right]\nabla_{\mathbf{w}}\hat{v}(s_t,\mathbf{w_t}) \end{aligned}\tag{2}\]

식 (2)는 식 (1)의 근사함수 버전이라고 할 수 있다. Table 1과 마찬가지로 가치함수 대신 여러가지 목표치를 사용할 수 있으며 그에 따라 근사화된 TD(0), Sarsa, Q-learning 등을 만들 수 있다. 근사함수로는 다양한 방법이 있으나 최근 딥러닝(deep learning)의 발달로 딥신경망(Deep Neural Network, DNN)을 근사함수(function approximator)로 활용하는 기법이 각광을 받고 있다.

4. Popular Algorithms

Deep Q-Network (DQN)

2015년 구글 딥마인드(DeepMind)가 네이처지에 발표한 논문{Mnih.2015}으로써 기존 Q-learning에 CNN(Convolutional Neural Network)을 접목시켜 아타리(Atari) 게임에서 인간의 실력을 능가하는 에이전트를 강화학습하는 알고리즘을 발표하여 놀라움을 주었다.

DQN은 딥러닝을 접목하여 end-to-end(센서의 raw data로부터 행동까지 전 과정을 처리하는) 방식의 에이전트를 얻어낸 성과 외에도 근사함수, 부트스트랩 및 비활성 정책 학습(off-policy training){Sutton.2018}을 사용하는 경우 기존 강화학습 알고리즘의 고질적인 발산 문제를 해결했다는 데에 의의가 있다. DQN의 핵심 아이디어는 다음과 같다.

• 경험재생(experience replay): 환경과의 상호작용 데이터를 메모리에 저장해두었다가 무작위로 미니배치(mini-batch)를 추출하여 학습함으로써 데이터간 상관관계(correlation)을 줄이는 기법
• 목표가치모델(target value function): 동일한 가치모델을 두 개 만든 후 행동가치모델(behavior value function)로는 샘플 데이터를 생성하고 목표가치함수(식 (1)의 $U_t$에 해당)는 느린 주기로 업데이트함으로써 목표가치함수를 안정화시키는 기법

---

1. 최적정책을 찾기 위한 반복작업(iteration)은 필요하다. ↩

2. 점추정(point estimation) ↩

3. 모집단 파라미터 $\theta$의 추정량 $\hat{\theta}$에 대한 편향은 $\mathbb{E}[\hat{\theta}]-\theta$로 정의된다. ↩

4. 이득 $G_t$은 정의에 의하여 $\mathbb{E}[G_t]-v_\pi(s_t)=v_\pi(s_t)-v_\pi(s_t)=0$이므로 불편추정량이다. $V_\pi(S_{t+1})$이 추정치이기 때문에 $\mathbb{E}[R_{t+1}+\gamma V_\pi(S_{t+1})]-v_\pi(s_t)\neq 0$이다. ↩

5. $G_t=R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+\cdots$에는 확률변수인 보상을 여러 번 더하므로 분산이 누적되지만 한 스텝의 보상만을 사용하는 $R_{t+1}+\gamma V_\pi(S_{t+1})$은 비교적 분산이 작다. (예로써 분산이 $\sigma_1^2, \sigma_2^2$인 두 정규분포를 갖는 확률변수의 합은 분산이 $\sigma_1^2 + \sigma_2^2$인 정규분포의 확률변수가 된다.) ↩