재미있게 살자

강화학습에서 가치함수법에 대한 연구가 활발히 진행되어 왔으나 가치함수 변화에 대하여 정책의 변화가 급격하다는 문제와 연속행동공간에서는 매 스텝마다 함수최적화를 풀어야 하는 문제1로 인하여 정책을 직접 구하는 정책경사법(policy-gradient methods){Sutton.2000}이 고안되었다.

가치함수법으로 만든 에이전트는 각 행동의 가치들을 산출하고 이로부터 하나의 행동을 선택하는 반면 정책경사법의 에이전트는 행동의 확률분포를 계산한 후 이로부터 하나의 행동을 샘플링한다.

\[a_t=\text{argmax}_a Q_\pi(s,a)\tag{가치함수법}\] \[a_t\sim\pi(a_t|s_t)\tag{정책경사법}\]

본 장에서는 정책경사법의 이론적 배경과 다양한 알고리즘을 살펴본다.

1. Policy-gradient theorem

정책경사법에서는 정책 $\pi(a|s)$가 에이전트의 출력이자 에이전트 그 자체를 나타낸다. 정책경사법의 에이전트는 주로 대형 스케일의 문제나 연속공간문제에서 활용되기 때문에 환경모델의 상태 개수보다 훨씬 적은 수의 파라미터 $\theta\ll|S|$를 갖는 근사함수 $\pi_\theta(a|s)$로 구현되어있다고 가정한다.

\[\pi_\theta(a|s)=\pi(a|s,\mathbf{\theta})=Pr(A_t=a|S_t=s,\mathbf{\theta}_t=\mathbf{\theta})\]

에피소딕 과정인 경우 정책을 향상시키기 위한 목적함수(objective function) $J(\mathbf{\theta})$로 정책 $\pi_\theta$가 주어졌을 때 초기상태의 가치인 $v_\pi(s_0)$을 사용할 수 있다.2 초기상태의 가치는 초기상태부터 종료상태까지 받는 모든 보상의 합의 기대값이므로 적절한 성능지표(performance measure)라고 할 수 있다.

\[J(\mathbf{\theta})\doteq v_\pi(s_0)\]

정책의 파라미터에 대한 목적함수를 미분하여 얻은 경사(gradient)를 이용하여 반복적으로 파라미터를 업데이트하면 최적의 정책을 찾을 수 있을 것이다. 가치함수법은 목적함수 값을 낮추는 것(gradient descent)이 목표라면 정책경사법은 목적함수 값을 높이는 것(gradient ascent)이 목표이다.

\[\mathbf{\theta}_{t+1}=\mathbf{\theta}_t+\alpha\nabla_{\mathbf{\theta}}J(\mathbf{\theta}_t)\tag{1}\]

목적함수가 기대값이기 때문에 경사를 엄밀히 계산하기 위해서는 무한히 많은 에피소드가 필요하다. 이는 현실적으로 불가능한 일이기 때문에 그 기대값이 경사를 근사하는 추정량(estimator)을 사용한다. 이러한 추정량을 찾기 위해 정책경사이론(policy-gradient theorem)인 식 (2){Sutton.2000}를 이용할 수 있다.

\[\begin{aligned} \nabla_{\mathbf{\theta}}J(\mathbf{\theta})&\propto\sum\limits_s\rho_\pi(s)\sum\limits_a q_\pi(s,a)\nabla_{\mathbf{\theta}}\pi_{\theta}(a|s) \\ &=\mathbb{E}_\pi\left[\sum\limits_a q_\pi(S_t,a)\nabla_{\mathbf{\theta}}\pi_{\theta}(a|S_t)\right] \end{aligned}\tag{2}\]

식 (2)에서 $\rho_\pi(s)$는 정책 $\pi_\theta$에 대한 정상상태분포(stationary state distribution)를 의미하며 $\mathbb{E}\pi$3는 정책 $\pi{\theta}$를 따르며 얻은 경로에 대한 기대값을 의미한다. 식 (2)에 약간의 트릭을 쓰면 식 (3)을 얻을 수 있다.

\[\begin{aligned} \nabla_{\mathbf{\theta}}J(\mathbf{\theta})&=\mathbb{E}_\pi\left[\sum\limits_a q_\pi(S_t,a)\nabla_{\mathbf{\theta}}\pi_{\theta}(a|S_t)\right] \\ &=\mathbb{E}_\pi\left[\sum\limits_a \pi_{\theta}(a|S_t) q_\pi(S_t,a)\frac{\nabla_{\mathbf{\theta}}\pi_{\theta}(a|S_t)}{\pi_{\theta}(a|S_t)}\right] \\ &=\mathbb{E}_\pi\left[q_\pi(S_t,A_t)\frac{\nabla_{\mathbf{\theta}}\pi_{\theta}(A_t|S_t)}{\pi_{\theta}(A_t|S_t)}\right] \\ &=\mathbb{E}_\pi\left[q_\pi(S_t,A_t)\nabla_{\mathbf{\theta}}\log\pi_{\theta}(A_t|S_t)\right] \\ \end{aligned}\tag{3}\]

결국 $q_\pi(s,a)\nabla_{\mathbf{\theta}}\log\pi_{\theta}(a\vert s)$를 $\nabla_{\mathbf{\theta}}J(\mathbf{\theta})$의 추정량으로 사용할 수 있다. 즉, 에피소드 경로 샘플로부터 $q_\pi(s,a)\nabla_{\mathbf{\theta}}\log\pi_{\theta}(a\vert s)$를 계산한 값으로 성능지표의 경사를 확률론적(stochastic)으로 구할 수 있으며 식 (1)을 반복함으로써 최적정책의 파라미터를 구할 수 있다.

2. Meaning of terms

앞에서 $q_\pi(s,a)\nabla_{\mathbf{\theta}}\log\pi_{\theta}(a|s)$이 목적함수의 경사값의 추정량으로 사용가능하다는 사실을 알게 되었다. 여기서 $\nabla_{\mathbf{\theta}}\log\pi_{\theta}(a|s)$는 상태 $s$일 때 행동 $a$를 선택할 확률 $\pi_\theta$의 $\log$ 값을 파라미터 $\theta$에 대하여 미분한 값이다. $\log$는 단조증가 함수이므로 $\pi_\theta$와 $\log\pi_\theta$의 변화하는 방향은 동일하다. $q_\pi(s,a)$는 정책 $\pi_\theta$에 따라 상태 $s$에서 행동 $a$를 선택할 때 얻을 수 있는 행동가치이다. $q_\pi(s,a)$와 $\nabla_{\mathbf{\theta}}\log\pi_{\theta}(a|s)$를 곱한다는 의미는 상태 $s$일 때 행동 $a$를 선택할 확률을 행동가치로 weighting을 조절한 값으로 파라미터 경사를 계산한다는 의미이다. 즉, 행동가치가 높을 경우 행동 $a$를 선택할 확률을 높이고, 행동가치가 낮을 경우 행동 $a$를 선택할 확률을 낮춘다는 의미이다. 아래에 설명할 어드밴티지 $A_\pi$를 이용하면 상태 $s$에서 행동 $a$를 선택할 때 양수 또는 음수의 상대가치를 곱하게 된다. 양수이면 상태 $s$일 때 행동 $a$를 선택할 확률을 높이고 반대로 음수이면 이를 낮추게 된다.
정책경사법을 구현할 때는 샘플 수집과 정책 업데이트를 교대로 반복하여 수행한다. 먼저 환경과의 상호작용을 통하여 샘플을 수집하며 이 때 가치(상태가치, 행동가치, 어드밴티지)와 $\log\pi_\theta$를 동시에 수집한다. 수집된 다수의 샘플로부터 가치와 $\log\pi_\theta$를 곱한 값을 서로 합하여 목적함수를 구성하고 미분을 통하여 정책 파라미터를 업데이트한다. 이때 가치는 고정된 값을 사용하고(torch.no_grad()) $\log\pi_\theta$만 미분한다.
결국 주어진 상태에서 특정한 행동을 선택할 확률을 높이거나 낮추기 위하여 가치 또는 어드밴티지를 weighted sum의 계수로 활용하는 것이다.

3. Baseline

정책은 확률분포이므로 그 합은 1이며 미분하면 0이 된다. 따라서 정책경사에 임의의 상태함수 $b(s)$를 곱하더라도 0이 된다. $b(s)$를 기준함수(baseline function)라고 한다.

\[\begin{aligned} \sum\limits_a b(s)\nabla_{\mathbf{\theta}}\pi_{\theta}(a|s) &=b(s)\nabla_{\mathbf{\theta}}\sum\limits_a\pi_{\theta}(a|s) \\ &=b(s)\nabla_{\mathbf{\theta}}1 \\ &= 0 \end{aligned}\tag{4}\]

식 (2), (3)와 (4)로부터 식 (5)를 얻을 수 있다. 기준함수를 사용하면 가치함수의 분산을 줄여 정책경사법을 안정화시켜준다.

\[\begin{aligned} \nabla_{\mathbf{\theta}}J(\mathbf{\theta}) &\propto\sum\limits_s\rho_\pi(s)\sum\limits_a \{q_\pi(s,a)-b(s)\}\nabla_{\mathbf{\theta}}\pi_{\theta}(a|s) \\ &=\mathbb{E}_\pi\left[\{q_\pi(s,a)-b(s)\}\nabla_{\mathbf{\theta}}\log\pi_{\theta}(A_t|S_t)\right] \\ \end{aligned}\tag{5}\]

기준함수로 상태가치함수 $v_\pi(s)$를 사용하면 $q_\pi(s,a)-b(s)$가 어드밴티지 $A_\pi(s,a)$가 된다.

\[\begin{aligned} \nabla_{\mathbf{\theta}}J(\mathbf{\theta}) &=\mathbb{E}_\pi\left[A_\pi(s,a)\nabla_{\mathbf{\theta}}\log\pi_{\theta}(A_t|S_t)\right] \\ \end{aligned}\tag{6}\]

4. Actor-Critic

식 (3) 또는 (5)를 이용하여 최적정책을 찾으려면 가치함수를 알아야 한다. {Sutton.1983}은 정책과 가치를 계산하는 두 개의 모델을 사용하여 정책경사를 추정하는 방법을 제시하였다. 정책을 계산하는 모델을 행동가(actor), 가치를 계산하는 모델을 비평가(critic)이라고 하며 두 모델을 사용하는 강화학습 알고리즘을 행동가-비평가(Actor-Critic, AC) 알고리즘이라고 한다. 비평가 모델을 $\Psi_t$라고 한다면 식 (7)의 일반화된 AC 알고리즘을 얻을 수 있다.{Schulman.2016} 식 (7)에서 $g$는 성능지표의 미분이며 상태공간에 대한 기대값을 시간에 대한 기대값으로 변환하였다.

\[\begin{aligned} g&\doteq\mathbb{E}_\pi\left[\sum\limits_{t=0}^\infty\Psi_t\nabla_{\mathbf{\theta}}\log\pi_{\theta}(a_t|s_t)\right] \\ \end{aligned}\tag{7}\]

비평가 모델 $\Psi_t$는 다음과 같이 다양한 형태로 구현할 수 있다.

  1. $G_0=\sum\limits_{t=0}^\infty r_t$: 경로에 대한 보상의 합
  2. $G_t=\sum\limits_{t’=t}^\infty r_{t’}$: 행동 $a_t$ 이후의 경로에 대한 보상의 합
  3. $\sum\limits_{t’=t}^\infty r_{t’}-b(s_t)$: 2번의 기준함수 버전
  4. $q_\pi(s_t,a_t)$: 행동가치함수
  5. $A_\pi(s_t,a_t)$: 어드밴티지 함수
  6. $r_t + \gamma v_\pi(s_{t+1})-v_\pi(s_t)$: TD 에러

5번의 어드밴티지를 이용하는 알고리즘을 어드밴티지 행동가-비평가(Advantage Actor-Critic) 알고리즘이라고 하며 줄여서 A2C라고 부른다. II 장에서 다룬 가치함수법은 비평가만 있는 critic-only 알고리즘이라고 생각할 수 있다.

a. Stochastic Policy-Gradient (SPG)

Figure 1은 확률론적 정책경사법(Stochastic Policy-Gradient, SPG){Sutton.2000}의 개념을 나타낸 그림이다. 환경에서 현재상태 $s_t$를 $\theta_t$ 파라미터의 정책모델과 $w_t$ 파라미터의 가치모델에 입력한다. 두 모델은 각각 행동공간에서의 확률분포 $\pi_\theta(\cdot|s_t)$와 행동가치값 $q_w(s_t,a_t)$를 출력한다. $\pi_\theta(\cdot|s_t)$으로부터 행동 $a_t$를 샘플링한 후 이를 다시 환경모델에 입력한다.

환경모델에서 얻은 보상 $r_{t+1}$과 행동가치값을 이용하여 다양한 가치함수법으로 비평가 목적함수 $J_c$를 구한다. Figure 1에서는 TD(0)를 이용하여 $J_c$를 구성하였다. $J_c$를 가치모델 파라미터 $w$에 대하여 미분함으로써 경사를 구하고 파라미터를 업데이트한다.

정책모델에서 얻은 행동 확률분포의 log 값을 $\theta$에 대하여 미분한 값과 $q_w$값을 곱하여 행동가 목적함수를 만든 후 $\theta$에 대하여 미분하여 파라미터를 업데이트한다.



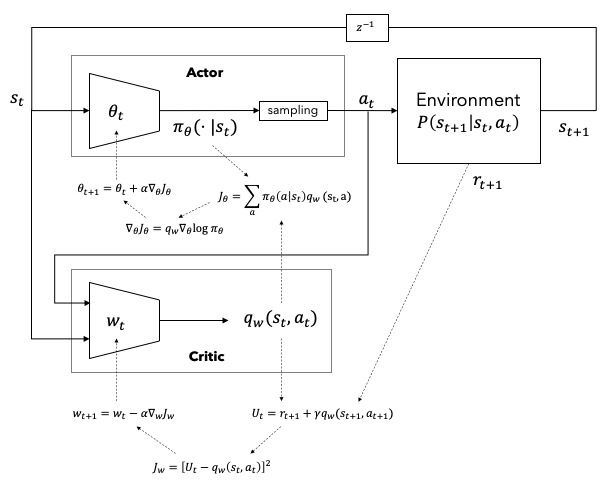
Figure 1. Stochastic Policy-Gradient (SPG)

b. Deterministic Policy-Gradient (DPG)

SPG는 정책모델이 확률분포를 출력해야 하기 때문에 연속행동공간에서 사용하기 어려운 단점이 있다. 이를 극복하기 위한 방법이 결정론적 정책경사법(Deterministic Policy-Gradient, DPG){Silver.2014}이다. Silver는 식 (8)과 같이 결정론적 정책모델이 출력하는 행동을 직접 미분하는 방법을 사용하여 Sutton의 정책경사이론과 유사한 이론을 도출하였다.

\[\begin{aligned} \nabla_{\theta}J(\mathbf{\theta}) &\doteq\mathbb{E}_\mu\left[\sum\limits_{t=0}^\infty\nabla_\theta q_\mu(s_t,\mu_\theta(s))\right] \\ &=\mathbb{E}_\mu\left[\sum\limits_{t=0}^\infty\nabla_a q_\mu(s_t,a)\big|_{a=\mu_\theta(s_t)}\nabla_{\mathbf{\theta}}\mu_{\theta}(a_t|s_t)\right] \\ \end{aligned}\tag{8}\]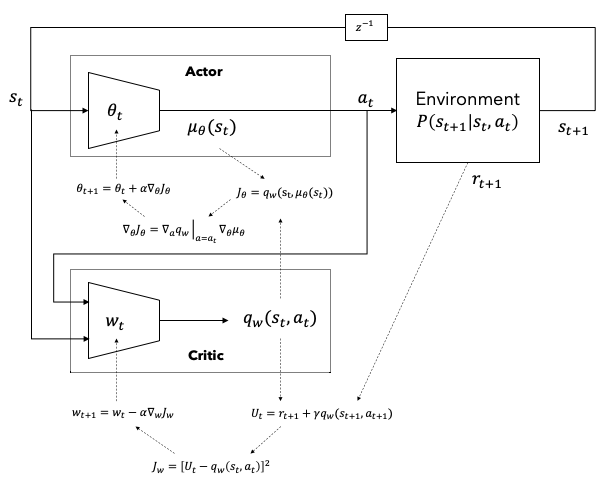


Figure 2. Deterministic Policy-Gradient (DPG)

  1. 이산행동공간을 다루는 실제 강화학습에서는 $Q_\pi(a_t\vert s_t)$를 $\mathbf{Q}_\pi(s_t)$ 형태로 변형하여 모든 행동에 대한 확률분포를 벡터형태로 한 번에 받을 수 있다. 하지만 연속행동공간인 경우 상태와 행동을 입력하면 그에 대한 가치를 얻는 $Q_\pi(s_t,a_t)$의 형태로 구성할 수 밖에 없다. 이러한 경우 $\text{argmax}_{a}Q_\pi(s_t,a)$를 구하기 위하여 함수최적화 문제를 풀어야 한다. ↩

  2. $v_\pi(s_0)=v_{\pi_{\theta}}(s_0)$ ↩

  3. $\mathbb{E}_\pi=\mathbb{E}_{\pi_{\theta}}$ ↩

You may also enjoy

Laplace Transform vs. z-Transform

 

• The Laplace Transform and $z$-Transform (along with other integral transforms such as the Wavelet Transform) are based on the concept of Hilbert spaces (ve...

Positive-definite Matrix

 

In linear algebra, an $n \times n$ Hermitian matrix $A$ is said to be positive definite if the scalar $x^{*}\text{Ax}$ is real and positive for all non-zero ...