강화학습: 개요(Introduction)

1. What is RL?

조금만 생각해보면 인간이 오래동안 먹지 못했을 때 배고픔을 느끼고 맛있는 음식을 먹었을 때 행복감을 느끼는 본능이 있기 때문에 음식으로부터 에너지를 얻고 생명을 유지한다는 것을 알 수 있다. 강화학습(reinforcement learning){Sutton.2018}은 인간이나 동물이 자신의 행동에 대한 환경의 보상에 따라 학습하는 과정을 모방하여 만든 기계학습의 한 분야이다.

Figure 1은 에이전트(agent)와 환경(environment)으로 이루어진 강화학습의 기본적인 구조를 나타낸다. 에이전트는 현재 상태(state) $s_t$를 입력받아 행동(action) $a_t$를 출력하고 환경은 그 행동에 영향을 받아 다음 상태 $s_{t+1}$로 변화한다. 이 때 보상(reward) $r_{t+1}$이 주어지는데 장기적인 보상의 합을 이득(return) $G$라고 한다. 에이전트는 장기적인 보상 합(이득)의 기대값을 최대화(to maximize the expected sum of long-term rewards) 하도록 학습된다. 이러한 학습을 강화학습이라고 한다.

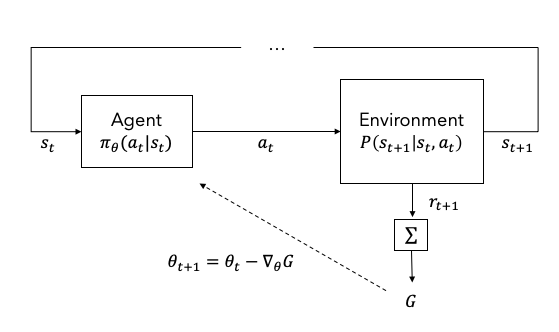
Figure 1. Basic architecture of RL

2. Agent and Policy

에이전트의 모든 가능한 행동의 집합을 행동공간(action space) $A$이라고 한다. 즉, $a\in A$이다. 행동공간이 이산적이면 이산 행동공간(discrete action space), 연속적이면 연속 행동공간(continuous action space) 이다. 테트리스 게임에서 좌우 이동버튼을 이산 행동공간이라고 할 수 있으며 자동차 운전시 조향핸들각과 페달변위를 연속 행동공간이라고 할 수 있다.

주어진 $s_t$에 대하여 $a_t$를 결정하는 에이전트의 행동방식을 정책(policy) 이라고 한다. 테트리스 게임에서 블록의 쌓여있는 형태와 내려오는 블록의 모양을 $s_t$라고 한다면 내려오는 블록을 좌우로 이동시키기 위한 명령을 $a_t$라고 할 수 있다. 정책은 높은 점수를 얻기 위하여 블록을 이동하는 방법이라고 할 수 있다.

정책은 결정론적 정책(deterministic policy){Silver.2014}과 확률론적 정책(stochastic policy){Sutton.2000}으로 구분할 수 있다. 결정론적 정책은 주어진 상태 $s_t$에 대하여 결정된 행동 $a_t=\mu(s_t)$를 출력한다.¹ Figure 2는 결정론적 정책의 예를 나타낸 그림이다. 행동공간에서 하나의 행동 $\mu(s_t)$에 대한 확률이 1이고 나머지 행동에 대한 확률은 0이다.

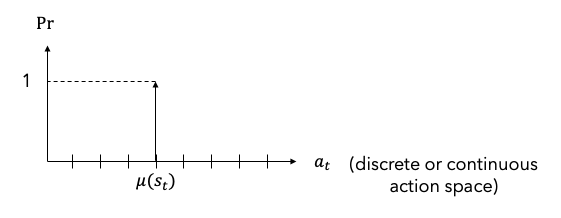
FIgure 2. Deterministic policy

\[\begin{aligned} Pr(A_t=\mu(s_t))&=1 \\ Pr(A_t\neq\mu(s_t))&=0 \end{aligned}\]

확률론적 정책에서는 행동 $a_t$가 확률변수(random variable)이며 확률분포(probability distribution) $\pi(a_t\vert s_t)=Pr(A_t=a_t\vert S_t=s_t)$를 따른다.^{2 3} 따라서 확률분포로부터 하나의 행동을 결정하기 위한 과정⁴이 추가적으로 필요하다. Figure 3은 확률론적 정책의 예이다. 위의 그래프는 이산 행동공간, 아래 그래프는 연속 행동공간에서의 확률분포이다. 합 또는 적분이 1이다.

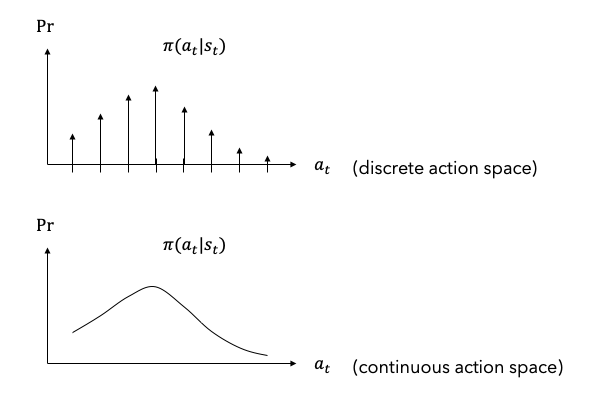
Figure 3. Stochastic policy

\[\begin{aligned} \sum\limits_{a_t\in A}\pi(a_t\vert s_t)&=1&\text{for discrete action space} \\ \int_{a_t\in A}\pi(a_t\vert s_t)da_t&=1&\text{for continuous action space} \end{aligned}\]

Why Long-term Rewards?

강화학습은 장기적 보상 합의 기대값(the expected sum of long-term rewards)을 최대화하기 위하여 에이전트의 정책을 학습하는 과정이라고 하였다. 왜 단기적인 보상이 아닌 장기적인 보상의 합을 최대화할까?

Figure 4는 장기적인 보상의 중요성을 설명하기 위한 하나의 예이다. 원시인이 그림 좌측의 갈래길에 있다고 하자. 원시인은 언제 다시 식량을 얻을 수 있을지 모르기 때문에 먹을 수 있는 과일이 있다면 최대한 수집해야 한다. 원시인의 가시거리는 점선원호로 표시한 곳까지 제한되며 한 번 지나간 길을 되돌아 갈 수 없다. 원시인은 어느 길을 선택해야 가장 많은 과일을 얻을 수 있을까? 출발지점에서는 가시거리의 제한으로 인하여 1번 길을 선택하는 것이 최선의 방법으로 보인다. 하지만 원시인이 여러 번 길을 되돌아 갈 수 있고 동일한 과일이 남아있다면 결국은 2번 길을 선택할 것이다. 이와 같이 단기적으로 유리해보이는 선택이 장기적으로 항상 유리한 선택이 아닐 수도 있기 때문에 장기적인 보상의 합이 중요한 것이다.

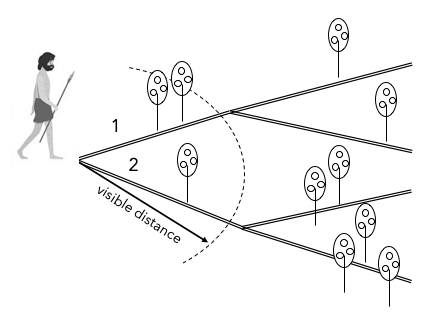
Figure 4. Why long-term rewards is important?

3. Environment and Model

환경(environment)은 에이전트의 행동이 영향을 미치는 대상으로서 에이전트로부터 행동 $a_t$를 받으면 환경의 현재 상태 $s_t$가 다음 상태 $s_{t+1}$로 변경된다. 환경의 모든 가능한 상태의 집합을 상태공간 $S$라고 한다. 즉, $s\in S$이다. 환경의 상태가 변하는 방식을 모델링한 것을 환경모델(environment model) 또는 모델(model) $P$라고 한다.

정책과 마찬가지로 모델도 결정론적 모델(deterministic model) 과 확률론적 모델(stochastic model) 로 구분할 수 있다. 결정론적 모델은 현재 상태 $s_t$와 행동 $a_t$에 따라 다음 상태 $s_{t+1}$이 하나로 결정되지만 확률론적 모델은 $s_{t+1}$이 확률변수이며 확률분포 $P(s_{t+1}\vert s_t,a_t)$를 따른다.

\[\begin{aligned} s_{t+1}&=P(s_t,a_t)&\text{deterministic model} \\ s_{t+1}&\sim P(s_{t+1}\vert s_t,a_t)&\text{stochastic model} \end{aligned}\]

강화학습에서 환경은 주로 이산시간 MDP(discrete-time Markov Decision Process) 로 모델링한다. 이산시간 MDP는 이산시간 마로코프 연쇄(discrete-time Markov chain)에 보상(reward) 과 선택(decision)을 추가한 모델로써 다음과 같이 순차적 결정 프로세스(sequential decision process) 를 모델링하는 데에 사용된다.

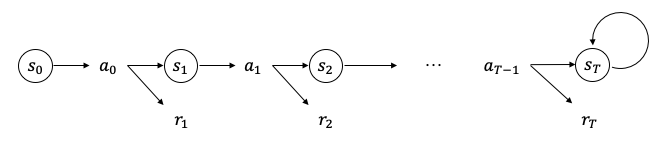
Figure 5. Sequential decision process

초기상태(initial state) $s_0$에서 행동 $a_0$를 선택하면 보상 $r_1$을 받고 상태 $s_1$으로 변경된다. 다시 행동 $a_1$을 선택하면 보상 $r_2$를 받고 상태 $s_2$로 이동한다. 이러한 과정을 반복하다가 종료상태(terminal state) $s_T$에 도달한다. 초기상태부터 종료상태까지의 과정을 에피소드(episode) 라고 한다. 에피소드에 끝이 존재하면 에피소딕(episodic)하다고 하며 끝이 없으면 연속적(continuing)이라고 한다. Figure 5와 같이 에피소딕 과정이 종료한 후에도 종료상태를 무한히 재방문한다고 가정하면 에피소딕 과정도 연속적 과정으로 생각할 수 있다.

현재 상태 $s_t$에서 받을 수 있는 이득 $G_t$의 정의는 식 (1)과 같다.⁵ $\gamma\in[0,1]$는 할인계수(discount factor) 이며 먼 미래의 보상에 대한 중요도를 줄여주는 역할을 한다. $\gamma$가 0이면 한 스텝 보상 $R_{t+1}$과 같아지며⁶ $\gamma$가 1이면 모든 보상을 동일한 중요도로 더한다는 의미이다. $\gamma^k R_{t+k+1}$을 할인된 보상(discounted reward)이라고 하며 할인계수를 고려한 MDP를 할인된 MDP(discounted MDP)라고 한다.

\[G_t\doteq\sum\limits_{k=0}^\infty \gamma^k R_{t+k+1}\tag{1}\]

연속적 과정인 경우 $\gamma\in[0,1)$이어야 유한한 이득을 얻을 수 있다.$\gamma<1$이면 어떤 시점 이후에는 보상이 무시할 수 있을 만큼 작은 값이 될 것이다. 이러한 시점을 지평선(horizon)이라고 부른다. 유한한 지평선(finite horizon)을 가정하면 연속적 과정도 에피소딕 과정처럼 다룰 수 있다.

종합적으로 말하자면 강화학습에서 주로 다루는 MDP 모델은 이산시간 유한 지평선 할인된 MDP(discrete-time finite-horizon discounted MDP)이다.

형식적으로는 MDP를 튜플(tuple) $<S,A,P,R,\rho_0,\gamma>$로 표현할 수 있다. 여기서 $S$는 상태공간, $A$는 행동공간, $P: S\times A\rightarrow(S\rightarrow [0,1])$⁷은 상태천이(state transition) 모델, $R: S\times A\times S\rightarrow \mathbb{R}$은 보상함수, $\rho_0: S\rightarrow [0,1]$⁷은 초기상태 확률분포, $\gamma\in[0,1]$은 할인계수를 의미한다.

초기상태 확률분포(initial state distribution) $\rho_0$는 에피소드를 시작할 때 처음 위치하는 상태의 방문확률(visitation probability)을 의미한다. 예를 들어, 테트리스 게임에서 게임을 시작할 때 처음 내려오는 다양한 블록의 상대빈도가 초기상태 확률분포이다.

고정된 정책이 주어지면 장시간 흐른 뒤 각 상태를 방문하는 상대빈도가 일정한 값에 수렴한다. 이를 정상상태 확률분포(stationary state distribution) $\rho(s)$라고 한다. 정상상태 확률분포는 초기상태 확률분포에 영향을 받지 않으며 강화학습에서 매우 중요한 개념이다.

Why MDP?

지도학습(Supervised Learning)은 각 샘플이 iid(independent and identically distributed) 한 것으로 가정한다. 하지만 강화학습의 환경에서 추출한 각 상태는 서로 독립적이지 않다. 예를 들어 테트리스에서 약 5초간 샘플한 블록의 위치들은 서로 연관되어 있다.

환경을 물리학의 시각으로 보면 시간에 따라 외부 입력에 의하여 상태가 변하는 동적시스템(dynamic system)이다. 동적시스템은 시간축으로 인접한 샘플이 독립적이지 않다.

일반적인 동적시스템은

\[\dot x = f(x,u)\tag{a}\]

로 표현할 수 있다. 식 (a)에서 $x$는 상태변수, $u$는 입력신호를 의미한다. 이를 이산화(discretize)하면 일차 차분방정식(first order difference equation)을 얻을 수 있다.

\[\frac{x_{t+1}-x_t}{\Delta t} = f(x_t, u_t)\] \[x_{t+1} = f(x_t, u_t) \Delta t + x_t\] \[x_{t+1} = F(x_t, u_t)\tag{b}\]

여기서 $F(x_t, u_t) = f(x_t, u_t)\Delta t + x_t$.

즉, 다음 상태의 값을 한 스텝 이전 상태와 입력신호의 함수로 표현할 수 있다. 이차 이상의 미분방정식으로 표현되는 시스템도 상태변수를 적절히 선택하면 일차 시스템으로 표현할 수 있다. 식 (b)는 결정론적 동적시스템을 표현한다. 즉, 현재 상태에 의하여 다음 상태가 결정된다. 모델의 불확실성이나 노이즈를 고려한다면 실제 동적시스템을 확률론적 동적시스템으로 표현해야 더 실제적이다. 따라서 확률론적 모델이 필요하다.

일차 차분방정식의 형태이며 확률론적 특성을 모델링하기 위해서는 MDP가 적절한 방식이라는 것을 알 수 있다.

Analogy between RL and Control Theory

강화학습에서 환경을 동적시스템으로 본다면 Table 1과 같이 강화학습과 제어이론(control theory)의 유사성을 찾을 수 있다.

Table 1. Analogy between RL and control theory

RL	Control Theory
환경	동적시스템 (플랜트)
에이전트	제어기
정책 $\pi$	제어 알고리즘
상태 $s$	상태 $x$ (센서 신호)
행동 $a$	제어명령 $u$ (액추에이터 제어신호)
전이확률행렬 $\mathbb{P}$	모델 $f()$ or $F()$ (지배방정식)
이득 $R$	목적함수 (objective function) 또는 손실함수 (loss function) c.f. 최적제어 (optimal control), MPC (Model Predictive Control)
초기상태 $\rho_0(s)$	초기상태 $x_0$ (initial condition)
정상상태 확률분포 $\rho(s)$	정상상태 응답 (steady-state response)

NOTE: 강화학습에서 사용하는 ‘알고리즘’ 용어는 제어 알고리즘을 의미하는 것이 아니라 최적정책을 찾기 위한 ‘학습방법’을 의미한다.

4. Value function

이득 $G_t$은 하나의 에피소드로부터 구하는 값이므로 현재 상태에서 미래에 받을 수 있는 모든 보상의 합을 대표하는 값이라고 할 수 없다. 이득의 기대값(expected value)이 보상의 합을 대표한다고 할 수 있을 것이다. 이득의 기대값을 가치함수(value function) 또는 가치(value) 라고 한다. 이득의 기대값은 상태의 함수이므로 가치함수라고 부른다.

정책 $\pi$가 주어졌을 때 상태 $s$로부터 시작하여 얻을 수 있는 이득의 기대값, 즉 상태가치(state value) $v_\pi(s)$는 식 (2)로부터 얻을 수 있다. 식 (2)의 마지막 등식은 상태가치 벨만방정식(Bellman equation for state value) 이라고 부른다.

\[\begin{aligned} v_{\pi}(s) &\doteq \mathbb{E}_\pi[G_t\vert S_t=s] \\ &= \mathbb{E}_\pi[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3} + \cdots\vert S_t=s] \\ &= \mathbb{E}_\pi[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3} + \cdots)\vert S_t=s] \\ &= \mathbb{E}_\pi[R_{t+1}+\gamma G_{t+1}\vert S_t=s] \\ &= \sum_{a}\pi(a\vert s)\sum_{s',r}p(s',r\vert s,a)\left[r+\gamma \mathbb{E}_\pi[G_{t+1}\vert S_{t+1}=s']\right] \\ &= \sum_{a}\pi(a\vert s)\sum_{s',r}p(s',r\vert s,a)[r+\gamma v_{\pi}(s')] \\ \end{aligned}\tag{2}\]

상태가치 벨만방정식은 Figure 6과 같은 백업 다이어그램(backup diagram) 으로 표현할 수 있다. 원은 상태, 점은 행동, 원에서 하나의 점을 선택하는 방법은 정책, 점에서 원으로의 이동은 환경의 상태천이와 보상을 나타낸다. 점에서 원으로의 화살표가 한 개이면 결정론적 모델이고 여러 개이면 확률론적 모델이다. 상태가치 벨만방정식은 현재 상태 $s$에서 한 스텝 후에 도달할 수 있는 모든 상태 $s’$의 가치를 이용하여 현재 상태의 가치를 구하는 식이다.

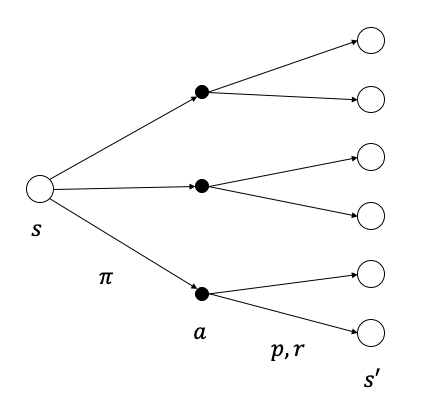
Figure 6. Backup diagram for state value

정책 $\pi$가 주어졌을 때 상태 $s$에서 행동 $a$를 선택한 이후의 과정에서 얻을 수 있는 이득의 기대값을 행동가치(action value) $q_\pi(s,a)$라고 하며 식 (3)을 이용하여 구할 수 있다. 식 (3)의 마지막 등식을 행동가치 벨만방정식(Bellman equation for action value) 이라고 한다.

\[\begin{aligned} q_{\pi}(s,a) &\doteq \mathbb{E}_\pi[G_t\vert S_t=s,A_t=a] \\ &= \mathbb{E}_\pi[R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3} + \cdots\vert S_t=s,A_t=a] \\ &= \mathbb{E}_\pi[R_{t+1}+\gamma G_{t+1}\vert S_t=s,A_t=a] \\ &= \sum_{s^\prime,r}p(s^\prime,r\vert s,a)[r+\gamma v_{\pi}(s')] \\ &= \sum_{s^\prime,r}p(s^\prime,r\vert s,a)[r+\gamma \sum_{a'}\pi(a'\vert s')q_{\pi}(s',a')] \end{aligned}\tag{3}\]

Figure 7은 행동가치 벨만방정식을 표현한 백업 다이어그램이다. 현재 상태에서의 행동가치 $q_\pi(s,a)$는 현재 상태-행동 조합 $(s,a)$에서 출발하여 한 스텝 후에 도달할 수 있는 모든 상태-행동 조합에 대한 행동가치를 이용하여 구할 수 있다.

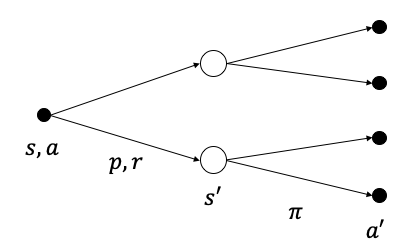
Figure 7. Backup diagram for action value

어드밴티지(advantage) $A$는 $q_\pi(s,a)$에서 $v_\pi(s)$를 뺀 값이다.

\[A(s,a)=q_\pi(s,a)-v_\pi(s)\]

어드밴티지는 상태가치에 대한 행동가치의 상대적 우수성을 나타낸다. 어떤 행동에 대한 어드밴티지가 양수이면 평균적인 가치(상태가치)보다 높은 이득을 획득할 수 있는 행동이며 음수이면 평균보다 낮은 이득을 얻을 수 있는 행동이라는 의미이다. 어드밴티지는 가치함수 업데이트를 위한 타겟(target)의 추정기(estimator) 중 분산이 가장 작은 것으로 알려져있기 때문에 최신 강화학습 알고리즘에서 최적정책을 찾기 위한 도구로 주목받고 있다.{Schulman.2016} SOTA(State-Of-The-Art) 알고리즘{Andrychowicz.2020}인 PPO(Proximal Policy Optimization){Schulman.2017}도 어드밴티지를 이용하여 최적정책을 찾는 알고리즘이다.

5. Optimal Policy

모든 정책을 포함하는 정책공간(policy space) $\Pi$가 있을 때 최적정책(optimal policy) $\pi^*$는 모든 상태와 모든 행동에 대한 가치가 다른 모든 정책보다 더 높거나 같은 정책을 의미한다. 임의의 이산시간 MDP에 대하여 적어도 한 개 이상의 최적정책이 존재한다.{Sutton.2018}

\[\begin{aligned} v^{\pi^*}(s)&\geq v^\pi(s)&\forall s\in S, \forall \pi\in \Pi \\ q^{\pi^*}(s,a)&\geq q^\pi(s,a)&\forall s\in S, \forall a\in A, \forall \pi\in \Pi \end{aligned}\]

MDP를 푼다는 것은 주어진 MDP에 대한 최적정책을 찾는 것을 의미한다. 결국 강화학습은 다음과 같은 최적화 문제라고 볼 수 있다.

1. MDP에 순차적인 행동을 인가하고 순차적인 상태를 획득하여 경로를 생성한다. (이와 같이 획득한 경로를 샘플(sample) 이라고 한다.)
2. 샘플에 대한 이득을 계산한다.
3. 1-2 과정을 반복한다.
4. 평균적인 이득을 높일 수 있는 행동방식(정책)을 찾는다.

간단한 MDP의 경우 모든 경로에 대한 이득을 계산하면 최적정책을 찾을 수 있다. 하지만 현실적인 문제에서는 경로의 수가 방대하여 쉽게 풀리지 않는다.

6. Why is RL difficult?

어떤 MDP의 행동공간 크기가 $b$이고 한 에피소드가 종료되기까지 $d$ 스텝이 소요된다면 경우의 수가 $b^d$인 경로가 존재할 것이다. 바둑의 경우 $b\approx 250, d\approx 150${Silver.2016}으로 현재의 컴퓨터 능력으로는 모든 상황에 대한 모든 수를 두어보는 것이 거의 불가능하다. 7자유도 로봇팔의 경우 연속적인 토크 또는 각도 명령 7개를 각 관절에 입력해주어야 하므로 행동공간 자체가 매우 방대하며 물건을 집는 간단한 작업일지라도 작업경로가 셀수 없을 정도로 많다는 것을 알 수 있다.

MDP의 최적정책을 찾기 위하여 모든 경로를 탐색하는 것은 바람직하지 않으며 많은 비용이 소요된다. 가급적 적은 수의 경로를 탐색한 후에 최적정책을 찾을 수 있다면 이상적이지만 가보지 않은 경로가 있다면 현재까지 찾은 정책이 최적정책이라고 확신할 수 없다. 결국 탐색을 더 해야하는지, 현재까지 찾은 정책을 활용해야 하는지의 문제가 발생한다. 이러한 문제를 탐색과 활용(exploration & exploitation) 문제라고 부른다.

결국 최적정책을 찾기 위하여 많은 수의 탐색이 필요하면서도 적은 수의 탐색이 요구되는 아이러니한 상황인 것이다. 이러한 문제를 해결하기 위한 노력을 다음 장부터 살펴본다.

7. Brief History of RL

• Until 1985: trial-and-error learning 개념 형성, 보상신호를 이용한 학습목표 달성
• Until 2010: 가치함수 및 근사화에 대한 연구 지배적
• 2015: DeepMind의 DQN{Mnih.2015}
  • CNN을 이용한 고차원 영상 end-to-end 처리
  • replay memory를 이용한 샘플 독립화
  • target model을 이용한 학습안정화
• 2015: DeepMind의 알파고 (MCTS 이용){Silver.2016}{Silver.2017}
• 2017: SOTA(State-Of-The-Art) 알고리즘 경쟁
  • 연속행동공간에 적용이 가능한 Actor-Critic이 대세
  • DeepMind 진영과 OpenAI 진영의 경쟁
  • DDPG{Lillicrap.2015}, A3C, TRPO{Schulman.2015} PPO{Schulman.2017} 등 유명
  • OpenAI John Schulman의 PPO 승리{Andrychowicz.2020}
• 현재: Sergey Levine (UC Berkely) 등이 로봇팔 제어를 포함하여 활발한 연구 진행 중

---

1. 결정론적 정책은 $\mu$, 확률론적 정책은 $\pi$로 표기한다. ↩

2. $a_t\sim\pi(a_t\vert s_t)$ ↩

3. 대문자 $S_t$, $A_t$는 확률변수를, 소문자 $s_t$, $a_t$는 샘플(표본)을 의미한다. ↩

4. 주로 확률분포 $\pi(a_t\vert s_t)$로부터 $a_t$를 샘플링(sampling)하는 방법을 사용한다. ↩

5. 보상 $R_t$는 확률변수를, $r_t$는 샘플을 의미한다. ↩

6. $0^0=1$로 가정한다. ↩

7. 연속상태공간일 때는 $S\rightarrow\mathbb{R}^+$ ($\mathbb{R}^+$= 양의 실수의 집합)으로 표현한다. ↩ ↩²